Teorema del triángulo isósceles

Advertencia: Esta instancia de uso es algo desconcertante cuando se ve por primera vez, así que se pide la cooperación cognitiva del lector. (El desconcierto se debe quizá a que el triángulo se pone en correspondencia consigo mismo, lo cual no está prohibido pero como que uno piensa que esa prohibición quedaba implícita en la definición de congruencia.)

Si un triángulo es isósceles entonces sus ángulos en la base son iguales. (Nota: se acostumbra entender por base, el tercer lado –los dos primeros son los que sabemos iguales.)

Demostración:
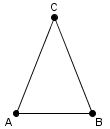El isósceles que se muestra puede llamarse triángulo ABC. Pero, recorriendo sus vértices en el sentido opuesto puede llamarse triángulo BAC.

Es pues válida la correspondencia $ABC \cong BAC$.       

Puesto que el triángulo es isósceles, CA=CB y BC=AC. También, como se trata del mismo triángulo, el ángulo formado en C es idéntico a sí mismo. Se tiene pues una correspondencia LAL y los dos triángulos son congruentes. Pero entonces los demás elementos puestos en correspondencia son también iguales. En particular el ángulo en A es igual al ángulo en B.

Segunda instancia de uso del criterio LAL

En un triángulo isósceles, la bisectriz del ángulo opuesto a la base divide al triángulo en dos congruentes.

Demostración:
En la figura de arriba trácese la bisectriz del ángulo C y suponga que corta al lado AB en M. Por hipótesis los ángulos ACM y MCB son iguales. Esto sugiere la correspondencia C-C. Por otro lado, también por hipótesis, AC=CB. Esto sugiere la correspondencia A-B, y el otro punto común a los triángulos formados por la bisectriz es M, lo cual sugiere la correspondencia M-M.

Así pues, probemos la correspondencia ACM-BCM. Tenemos, AC=BC y CM=CM, falta ver si el ángulo formado por AC y CM es igual al formado por BC y CM. Pero eso es cierto por ser CM bisectriz. Así que podemos usar el criterio LAL para establecer que los triángulos puestos en correspondencia son congruentes.

De esta congruencia así establecida se siguen varios

Corolarios (para isósceles):

1. La bisectriz es también mediatriz (pues los ángulos AMC y BMC son iguales y su suma es un llano, pero también los lados correspondientes AM y BM son iguales, así que MC es la perpendicular por el punto medio del la base)
    
2. La bisectriz es también mediana (pues AM=BM)
    
3. La bisectriz es también altura (pues los ángulos AMC y BMC son rectos)