Publicaciones Recientes
Sobre la teoría de reificación de Anna Sfard
Trigonometría en el examen ENLACE 2010
A pesar de que en el aula nunca se haya abordado un tema, si ese tema está en el programa entonces seguramente habrá un reactivo en el examen ENLACE que lo necesite para resolverlo. Es el caso de la ley de cosenos: $a^2=b^2+c^2-2bccosA $ (donde A es el ángulo formado por los lados $b$ y $c$ de un triángulo).
Cuadrilátero completo y puntos medios de sus diagonales
Consideremos $a$, $b$, $c$ y $d$ cuatro rectas no tres de ellas concurrentes (es decir, un cuadrilátero completo) y no dos de ellas paralelas. Demuestra que son colineales los puntos medios de las tres diagonales del cuadrilátero completo.
Nota: Las diagonales de un cuadrilátero completo son los segmentos que unen un punto de intersección de dos de sus lados con el de los otros dos lados.
Comentarios finales
Se puede deducir el criterio LLL a partir del LAL aplicando las propiedades del triángulo isósceles: los triángulos en correspondencia LAL se colocan como se muestra en la figura y…
Puesto que AB=IJ y AB=IK, tenemos los isósceles ABI y ACI. Pero entonces sus ángulos en la base son iguales.
Sumando, se obtiene que los ángulos en A y en I son iguales y estamos ya en posibilidad de aplicar el criterio LAL para asegurar que los triángulos ABC e IJK son congruentes.
Un teorema de medianas
La demostración del siguiente teorema es instructiva de cómo un trazo auxiliar permite el uso de resultados elementales (en este caso congruencia de triángulos) en la solución de problemas geométricos.
Pero también nos enseña el razonamiento en reversa, muy útil en la demostración de teoremas geométricos del tipo “si y sólo si.” No está de más añadir que lo más instructivo de las demostraciones de los teoremas elementales de geometría es la construcción de las figuras.
Segundo teorema de la línea media
La paralela a la base que pasa por el punto medio de un lado pasa también por el punto medio del otro lado.
Demostración:
Otra vez el trazo auxiliar que ayuda a la demostración es clásico y muy instructivo. Sea ABC el triángulo y N el punto medio de AC. Por N tracemos una paralela NM a la base BC. Vamos a demostrar que M es punto medio de AC.
El trazo auxiliar consiste en el segmento que une N con el punto medio K de la base BC. Este trazo nos permite aplicar el primer teorema de la línea media y asegurar KN//AB y KN=AB/2. Pero entonces:
Primer teorema de la línea media
La línea media de un triángulo es paralela a la base y mide la mitad de ésta.
Demostración:
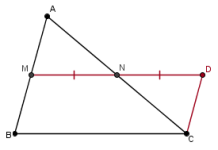
Tracemos la línea media MN de los lados AB y AC del triángulo ABC. El trazo auxiliar que necesitamos es prolongar MN hasta D de tal manera que MN=ND. (Nota: la demostración es clásica y es instructiva de cómo usar trazos auxiliares en la solución de problemas geométricos.)
Los triángulos MNA y DNC son congruentes (criterio LAL).
Teoremas de la línea media
El segmento que une los puntos medios de dos lados de un triángulo es paralelo al tercero y mide la mitad de éste.
Este es un teorema muy útil en la solución de problemas geométricos. De hecho se trata de dos teoremas de la línea media (el otro dice: paralela a la base por punto medio pasa por el punto medio) y pueden ser demostrados usando trazos auxiliares para formar triángulos congruentes.
Segunda instancia de uso del criterio LAL
En un triángulo isósceles, la bisectriz del ángulo opuesto a la base divide al triángulo en dos congruentes.
Demostración:
En la figura de arriba trácese la bisectriz del ángulo C y suponga que corta al lado AB en M. Por hipótesis los ángulos ACM y MCB son iguales. Esto sugiere la correspondencia C-C. Por otro lado, también por hipótesis, AC=CB. Esto sugiere la correspondencia A-B, y el otro punto común a los triángulos formados por la bisectriz es M, lo cual sugiere la correspondencia M-M.
Teorema del triángulo isósceles
Advertencia: Esta instancia de uso es algo desconcertante cuando se ve por primera vez, así que se pide la cooperación cognitiva del lector. (El desconcierto se debe quizá a que el triángulo se pone en correspondencia consigo mismo, lo cual no está prohibido pero como que uno piensa que esa prohibición quedaba implícita en la definición de congruencia.)
Si un triángulo es isósceles entonces sus ángulos en la base son iguales. (Nota: se acostumbra entender por base, el tercer lado –los dos primeros son los que sabemos iguales.)

