Coloración propia de gráficas

Una coloración propia  o buena coloración de una gráfica G consiste es una asignación de colores a los vértices de la gráfica de tal manera que vértices unidos por una arista tengan distinto color.

Formalmente,  una coloración propia de una gráfica G es una asignación de colores a los vértice de G de manera que para cualesquiera $u,v \in V(G)$ con $uv \in A(G)$, el color de $u$ es distinto al color de $v$.

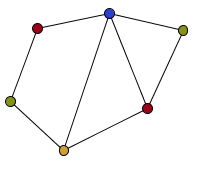
Por ejemplo, en la figura de la izquierda se muestra una gráfica con una coloración propia con 5 colores y  en la de la derecha la misma gráfica con una coloración propia de 4 colores.

A una coloración que usa $m$ colores se le llama $m$-coloración propia.  A la menor cantidad de colores necesarios para colorear una gráfica $G$ se le llama número cromático de $G$ y se denota con $\chi(G)$.

NOTA: Es usual que en lugar de asignar colores a las aristas se les asignen números enteros $\{1, 2, 4, \ldots \}$. Esto es debido a que después de 6, 7 u 8 colores ya es complicado pensar en colores y resulta más fácil pensar en "color uno", "color dos", "color tres", etcétera o bien sólo 1, 2, 3, etcétera.