

A lo largo de este capitulo veremos la definición de congruencia y algunos usos prácticos en la argumentación para la solución de problemas.
La congruencia no la definiremos formalmente si no hasta la sección "Congruencia de triángulos como noción intuitiva y su formalización [1]".
El concepto de congruencia está emparentado con el de igualdad y se espera que el aprendiz la conozca ya sea por su significado intuitivo a partir del lenguaje natural, o bien a través de su uso en la aritmética.
Es costumbre que en geometría se hable de congruencia en vez de igualdad. Por ejemplo dos segmentos son congruentes si y sólo si tienen la misma medida –y lo mismo es cierto para ángulos. Pero en el caso de dos triángulos la definición es más complicada pues no hay una medida (número) que defina a un triángulo.
Intuitivamente, dos triángulos se dice que son congruentes si todas sus medidas correspondientes son iguales: lados, ángulos, áreas, etcétera . Por ejemplo, en la siguiente figura se muestran tres triángulos congruentes:

Una posible razón razón al uso de la palabra congruencia en lugar de igualdad, es para remarcar que los triángulos pueden ser distintos, es decir, tienen todas sus medidas iguales, pero su posición y orientación en el plano pueden ser muy diferentes.
Como se sabe, hay diversas clasificaciones de triángulos que dan cuenta de su diversidad de forma: de acuerdo a la medida de sus ángulos pueden ser obtusángulos [2], rectángulos [3], acutángulos [4]; de acuerdo a la relación de las medidas de sus lados pueden ser equiláteros [5], isósceles [6], escalenos [7]. Es por eso que una noción previa a la definición de congruencia de triángulos es la de correspondencia. Y esto porque un triángulo (y cualquier polígono [8]) es una configuración que consiste de puntos y segmentos de recta (lados) que unen pares de puntos.
Decir que el triángulo $ABC$ está en correspondencia con el $PQR$ significa que la correspondencia entre sus vértices es $A \to P$, $B \to Q$ y $C \to R$. Y en esta correspondencia queda implícita la correspondencia entre sus lados: $AB \to PQ$, $BC \to QR$ y $CA \to RP$. Pero también queda implícita la correspondencia entre sus ángulos: el ángulo en $A$ (o bien, $\angle BAC $) corresponde al ángulo en $P$ (o bien, $\angle QPR$), etcétera.1

1). No todos los textos siguen esta convención, es decir, aun cuando afirmen “$ABC$ está en correspondencia con $IJK$” no respetan las reglas anteriores de las correspondencias implícitas –una lástima… pero qué se le va a hacer.
Después de haber descubierto el hecho de que dos triángulos son congruentes (iguales) es conveniente poner sus vértices en correspondencia.
Y cuando digo “descubierto” quiero decir que el cognizador descubre la congruencia por métodos intuitivos e informales, o quizá sea mejor decir, “la ve”. Pero una vez que “ve” la congruencia es conveniente formalizarla. Es conveniente porque una vez establecida la correspondencia de congruencia (en la forma en que se explica en la sección anterior [9]) ya no es necesario ver la figura para plantear ecuaciones o razones, pues como ya se explicó, las correspondencias entre ángulos y lados quedan implícitas en la correspondencia entre los triángulos.
Para poder ver la congruencia es necesario buscarla, es decir, algo (una frase, un dato,…) en el enunciado del problema debe sugerir que se puede usar congruencia para su solución. Y para encontrarla, una vez que se está buscando, es conveniente usar la definición intuitiva: dos triángulos son congruentes si pueden hacerse coincidir uno sobre el otro mediante giros, traslaciones y/o reflexiones.
La definición formal es:
Dos triángulos son congruentes si, existe una correspondencia entre sus vértices, de tal manera que lados y ángulos correspondientes son iguales.
Y se denotará así $ABC \cong PQR$ para indicar que el triángulo $ABC$ es congruente al triángulo $PQR$.
En una congruencia de triángulos entonces se tienen seis igualdades, tres lados y tres ángulos. Es por eso muy útil tener criterios que nos digan si dos triángulos son congruentes sin tener que verificar las seis igualdades.
Los criterios o principios de congruencia nos dicen cómo determinar si dos triángulos son congruentes sin necesidad de verificar las seis igualdades entre lados y ángulos correspondientes.
Criterio LAL (Lado-ángulo-lado). Es posiblemente el criterio de congruencia más básico, este criterio nos dice que si, en una correspondencia de triángulos, dos lados de uno y el ángulo comprendido entre ellos son iguales a sus correspondientes elementos en el otro, entonces los dos triángulos son congruentes.

Algunos textos de geometría –los más formales, en el sentido lógico— toman este criterio como axioma y demuestran los dos restantes, el ALA y el LLL. Otros textos –la mayoría— postulan como verdaderos los tres criterios. Es recomendable entonces que el aprendiz tome los tres como postulados pues, si de cualquier manera se va a tomar uno como postulado…
Criterio LLL (Lado-lado-lado). Este criterio afirma que si en una correspondencia de triángulos los lados correspondientes son iguales, entonces los triángulos serán congruentes.

Criterio ALA (Ángulo-lado-ángulo). Si en una correspondencia de triángulos, dos ángulos en uno de ellos y el lado común son iguales sus correspondientes del otro triángulo, entonces los triángulos serán congruentes.

Mostraremos ahora algunos problemas ejemplo donde resulta útil el criterio de congruencia LAL. Se le invita al lector a intentar primero resolver los ejercicio planteados y posteriormente leer la solución propuesta.
Advertencia: Esta instancia de uso es algo desconcertante cuando se ve por primera vez, así que se pide la cooperación cognitiva del lector. (El desconcierto se debe quizá a que el triángulo se pone en correspondencia consigo mismo, lo cual no está prohibido pero como que uno piensa que esa prohibición quedaba implícita en la definición de congruencia.)
Si un triángulo es isósceles entonces sus ángulos en la base son iguales. (Nota: se acostumbra entender por base, el tercer lado –los dos primeros son los que sabemos iguales.)
Demostración:
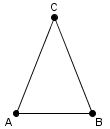 El isósceles que se muestra puede llamarse triángulo ABC. Pero, recorriendo sus vértices en el sentido opuesto puede llamarse triángulo BAC.
El isósceles que se muestra puede llamarse triángulo ABC. Pero, recorriendo sus vértices en el sentido opuesto puede llamarse triángulo BAC.
Es pues válida la correspondencia $ABC \cong BAC$.
Puesto que el triángulo es isósceles, CA=CB y BC=AC. También, como se trata del mismo triángulo, el ángulo formado en C es idéntico a sí mismo. Se tiene pues una correspondencia LAL y los dos triángulos son congruentes. Pero entonces los demás elementos puestos en correspondencia son también iguales. En particular el ángulo en A es igual al ángulo en B.
En un triángulo isósceles, la bisectriz del ángulo opuesto a la base divide al triángulo en dos congruentes.
Demostración:
En la figura de arriba trácese la bisectriz del ángulo C y suponga que corta al lado AB en M. Por hipótesis los ángulos ACM y MCB son iguales. Esto sugiere la correspondencia C-C. Por otro lado, también por hipótesis, AC=CB. Esto sugiere la correspondencia A-B, y el otro punto común a los triángulos formados por la bisectriz es M, lo cual sugiere la correspondencia M-M.
Así pues, probemos la correspondencia ACM-BCM. Tenemos, AC=BC y CM=CM, falta ver si el ángulo formado por AC y CM es igual al formado por BC y CM. Pero eso es cierto por ser CM bisectriz. Así que podemos usar el criterio LAL para establecer que los triángulos puestos en correspondencia son congruentes.
De esta congruencia así establecida se siguen varios
Corolarios (para isósceles):
El segmento que une los puntos medios de dos lados de un triángulo es paralelo al tercero y mide la mitad de éste.
Este es un teorema muy útil en la solución de problemas geométricos. De hecho se trata de dos teoremas de la línea media (el otro dice: paralela a la base por punto medio pasa por el punto medio) y pueden ser demostrados usando trazos auxiliares para formar triángulos congruentes.
Estas demostraciones son muy instructivas para el aprendiz pues, además de ser instancias de uso de la congruencia de triángulos, dejan una lección sobre las condiciones que debe cumplir un cuadrilátero para ser paralelogramo. (Línea media se acostumbra llamar al segmento que une los puntos medios de dos lados de un triángulo.)
La línea media de un triángulo es paralela a la base y mide la mitad de ésta.
Demostración:
Tracemos la línea media MN de los lados AB y AC del triángulo ABC. El trazo auxiliar que necesitamos es prolongar MN hasta D de tal manera que MN=ND. (Nota: la demostración es clásica y es instructiva de cómo usar trazos auxiliares en la solución de problemas geométricos.)
 Los triángulos MNA y DNC son congruentes (criterio LAL).
Los triángulos MNA y DNC son congruentes (criterio LAL).
De aquí que los ángulos MAN y NCD son guales. Como son alternos internos se concluye que CD//MB. También por congruencia, MA=DC.
Pero entonces tenemos que MBCD es paralelogramo (dos opuestos iguales y paralelos). Así que, como MBCD es paralelogramo, se puede concluir que MN//BC y 2MN=BC, como se quería.
Comentario:
Es conveniente que el lector practique en otros ejercicios los argumentos “alternos internos iguales, luego paralelas” y “lados opuestos iguales y paralelos, luego paralelogramo” (de paso puede demostrar esto último usando un argumento de congruencia de triángulos).
La paralela a la base que pasa por el punto medio de un lado pasa también por el punto medio del otro lado.
Demostración:
Otra vez el trazo auxiliar que ayuda a la demostración es clásico y muy instructivo. Sea ABC el triángulo y N el punto medio de AC. Por N tracemos una paralela NM a la base BC. Vamos a demostrar que M es punto medio de AC.
El trazo auxiliar consiste en el segmento que une N con el punto medio K de la base BC. Este trazo nos permite aplicar el primer teorema de la línea media y asegurar KN//AB y KN=AB/2. Pero entonces:
--son iguales los ángulos KNC y MAN (por ser correspondientes),
--son iguales los ángulos CKN y NMA (por tener lados paralelos),
--NC=AN (por hipótesis).
(Datos: AN=NC, NM//BC, BK=KC.)
Conclusión: Los triángulos AMN y NKC son congruentes (criterio LAA).
De aquí que KN=AM. Pero, por ser línea media, 2KN=AB. Es decir, 2AM=AB como se quería.
(Nota: podría argumentarse también que KN=MB por ser MNKB paralelogramo, y…)
La demostración del siguiente teorema es instructiva de cómo un trazo auxiliar permite el uso de resultados elementales (en este caso congruencia de triángulos) en la solución de problemas geométricos.
Pero también nos enseña el razonamiento en reversa, muy útil en la demostración de teoremas geométricos del tipo “si y sólo si.” No está de más añadir que lo más instructivo de las demostraciones de los teoremas elementales de geometría es la construcción de las figuras.
El aprendiz debería aprovechar la oportunidad para afinar sus habilidades en la construcción de figuras geométricas –y su profesor debería darle la ayuda ajustada. Y ahora que digo esto voy a detallar la construcción de la figura, aunque sea sólo por esta vez.
Teorema de las medianas del isósceles:
Un triángulo es isósceles si y sólo si dos de sus medianas son iguales.
Demostración:
Vamos a demostrar primero la parte “sólo si” (isósceles sólo si medianas iguales). Lo primero que hago es dibujar un isósceles ABC y los puntos medios M y N de los lados AB y AC, respectivamente. (Lo siento, no puedo detallarlo tanto; si el lector no sabe cómo construir un isósceles y/o un punto medio, debería dedicarle una o dos tardes al dibujo geométrico elemental.)
Ya con los puntos medios trazo las medianas BN y CM y llamo G a su intersección.
Vamos a demostrar que BN=CM. Esta parte es la fácil. Porque los ángulos en la base de un isósceles son iguales y ello nos permite identificar los triángulos congruentes MBC y NCB (criterio LAL). De aquí que CM=BN.
La parte del “si” (dos medianas iguales entonces isósceles) es la más difícil.
El trazo auxiliar que aporta la perspectiva adecuada para “ver” el resultado no es obvio. Pero es clásico. Así que el aprendiz debe tomarlo como ejemplo para posibles aplicaciones posteriores.
Prolongo las medianas hasta los puntos M’ y N’ de tal manera que GM=MM’ y GN=NN’. La idea es formar congruentes opuestos por el vértice, un artificio que ya conocemos.
(Los círculos los dejé para hacer transparente la forma en que se traza con compás un segmento sobre una recta de longitud dada.)
Ocultando los círculos y mostrando sólo lo que se va a necesitar, la figura quedaría como se muestra.
Ahora trazo los segmentos M’B y N’C para formar dos pares de triángulos congruentes (según criterio LAL): M’MB y GMA, N’NC y GNA.
El hallazgo clave aquí es M’B=N’C (puesto que ambos segmentos son iguales a GA) y M’B//N’C (pues ambos son paralelos a GA, por triángulos alternos internos iguales).
Pero, “opuestos iguales y paralelos, luego paralelogramo”…
He aquí los paralelogramos: M’BCN’, M’BGA y N’CGA.
Las diagonales del paralelogramo se bisecan ¿no es cierto?
Tenemos pues que BG=GN’=2GN y CG=GM’=2GM. Ahora sólo necesitamos asegurar GM=GN.
Por hipótesis BN=CM. Es decir, 2GN+GN=BN=CM=2GM+GM. O sea, GN=GM.
Así que los paralelogramos M’BGA y N’CGA tienen sus lados correspondientemente iguales y las diagonales correspondientes GN’ y GN’ son también iguales. Por lo tanto las otras dos diagonales correspondientes BA y CA deben ser iguales. En otras palabras, el triángulo ABC es isósceles.
Se puede deducir el criterio LLL a partir del LAL aplicando las propiedades del triángulo isósceles: los triángulos en correspondencia LAL se colocan como se muestra en la figura y…
Puesto que AB=IJ y AB=IK, tenemos los isósceles ABI y ACI. Pero entonces sus ángulos en la base son iguales.
Sumando, se obtiene que los ángulos en A y en I son iguales y estamos ya en posibilidad de aplicar el criterio LAL para asegurar que los triángulos ABC e IJK son congruentes.
Digamos, para finalizar, que la noción de congruencia de triángulos está muy cerca de los fundamentos de la geometría euclidiana. Pero el aprendiz no necesita justificar todo, sobre todo los teoremas cercanos a los fundamentos: Es mejor, desde el punto de vista de solución de problemas, que tome los criterios de congruencia como axiomas y los use sin ningún remordimiento en la solución de problemas. Esto le permitirá avanzar en su apropiación de herramientas teóricas sin perder tiempo en formalismos. También como dado se debe tomar la igualdad de ángulos formados por dos paralelas y una transversal. Desde luego que es conveniente que alguna vez vea las demostraciones de los teoremas básicos, pero eso puede esperar… Mientras tanto, que resuelva problemas…
Enlaces:
[1] https://www.matetam.com/../../../../../../de-consulta/books/geometria-basica-principiantes/congruencia-triangulos-como-nocion-intuitiva-y-su-f
[2] https://www.matetam.com/glosario/definicion/triangulo-obtusangulo
[3] https://www.matetam.com/glosario/definicion/triangulo-rectangulo
[4] https://www.matetam.com/glosario/definicion/triangulo-acutangulo
[5] https://www.matetam.com/glosario/definicion/triangulo-equilatero
[6] https://www.matetam.com/glosario/definicion/triangulo-isosceles
[7] https://www.matetam.com/glosario/definicion/triangulo-escaleno
[8] https://www.matetam.com/glosario/definicion/poligono
[9] https://www.matetam.com/de-consulta/books/geometria-basica-principiantes/triangulo-como-configuracion-puntos-y-rectas