Ana, Beto y Carlos decidieron jugar unas retas de ajedrez: al terminar una partida, el que estaba esperando entraba a jugar contra el ganador. Empezaron las retas con una partida entre Ana y Beto. Al final de varias partidas, Ana acumuló 17 victorias; Beto, 14 y Carlos no contó las suyas.
¿En cuántas partidas se enfrentaron Ana y Beto?
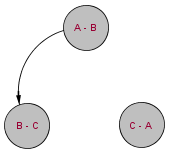
Para explicar la solución construyamos un diagrama para el desarrollo de las partidas. Empecemos colocando un vértice por cada pareja de oponentes; Ana vs Beto (A-B), Beto vs Carlos (B-C) y Carlos vs Ana (C-A). Luego por cada juego jugado, ponemos una flecha que va desde la pareja que jugó hacia la pareja que va jugar. En la siguiente figura se muestra como quedaría el diagrama si en el primer juego (que por dato es el de Ana contra Beto) ganara Beto, en tal caso seguiría el juego entre Beto y Carlos, por eso se traza una flecha de A-B a B-C.
 |
|
Figura 1. |
Como se puede ver la flecha nos dice no sólo quienes jugaron y quienes jugarán después, además nos dice quién gano: Si la flecha une A-B con B-C (no importa donde halla empezado) es un juego ganado por Beto; si la flecha une B-C con C-A, es un juego ganado por Carlos; y si une A-B con C-A es un juego ganado por Ana.
 |
|
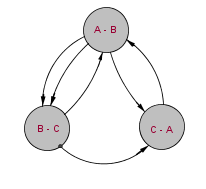
Figura 2. La siguiente imagen muestra cómo se vería nuestro gráfico si el orden sucesivo de los ganadores en unas retas hubiera sido así: Beto, Carlos, Ana, Beto, Beto y Ana. |
Entonces, el total de flechas que estén entre el vértice A-B y el B-C son los juegos ganados por Beto; y el total de flechas entre A-B y C-A son los jeugos ganados por Ana. En consecuencia, la cantidad de flechas que terminan o salen de A-B son la suma de los juegos ganadas de Beto más los de Ana.
Por último, notemos que las flechas del diagrama pueden ser recorridas de forma continua (sin dar saltos) y respetando la dirección de las flechas. Esto pues, al final de cuentas, las flechas nos dicen cuál es el juego siguiente.
Ahora bien, la cantidad de flechas que salen del vértice A-B es exactamente lo que deseamos calcular: la cantidad de juegos disputados entre Ana y Beto. Por hipótesis del problema, la primera flecha sale de A-B. Ahora bien, al ir recorriendo las flechas, para que en el camino se dibujase una flecha que sale de A-B, primero tiene que dibujarse una que llegue a A-B. En resumen, exceptuando la primera flecha, por cada flecha que sale hay otra que entra. Entonces, las flechas que salen se agrupan en parejas con las que entran. Entonces, si N es el número de las flechas que salen, existen N-1 flechas que entran. Ahora, podría ocurrir que al final entrara una flecha y nunca saliera, en tal caso, habría N flechas que entran.
Entonces, tenemos que podría haber 2N flechas que salen o entran de A-B, o bien, puede haber 2N-1 (dependiendo si en el último juego que se jugó perdió Carlos o no, es decir, la última flecha termina en A-B o no) .
Por último, como la suma de los juegos ganados por Ana más los de Beto es impar (17 + 14 = 31), entonces, estamos en el caso en que la última flecha no termina en A-B. Por lo tanto, 2N -1 = 31, por ende, N = 16.
Hubo 16 juegos entre Ana y Beto.
