Figura geométrica formada por cuatro rectas no tres de ellas concurrentes.

Este concepto es perteneciente a la rama de la geometría proyectiva. Pero puede entenderse fácilmente sin ella, sólo hay que desechar la siguiente posibilidad:
- Tres rectas paralelas y una cuarta transversal a éstas NO forman un cuadrángulo completo.
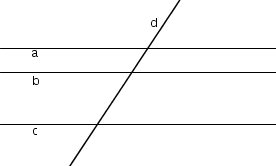
La razón por la que se tiene que desechar este caso es que en el campo de la geometría proyectiva se considera que tres rectas paralelas concurren en un punto al "infinito". (Ver el libro Introducción a la geometría proyectiva)
Esta concepto es el dual al de cuadrángulo completo: cuatro puntos no tres de ellos colineales.
La principal diferencia entre el cuadrángulo y cuadrilátero completos es que con las cuatro rectas se definen seis puntos (la intersección de cada par de rectas) y en el cuadrángulo sólo hay cuatro puntos. Aunque, de manera dual, los cuatro puntos del cuadrángulo definen seis rectas, la unión de cada par de puntos.
