Publicaciones Recientes
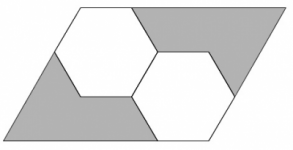
La región complemento de dos hexágonos
En la siguiente figura tenemos dos hexágonos con sus lados iguales. El paralelogramo tiene área de 2016 u2 , ¿cuál es el área de la región sombreada?
Capacidad del estadio de futbol
Al inicio de un partido de futbol, al estadio estaba al 30% de capacidad, 30 minutos después había 3000 aficionados más que al inicio y al estadio le faltaba un 30% para llenarse, ¿cuál es la capacidad del estadio?
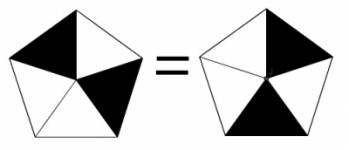
Coloreado de pentágono
Problema 1. En el pizarrón hay dibujado el siguiente pentágono. Paty tiene dos colores distintos, blanco y negro. ¿Cuántos pentágonos distintos podría obtener usando sus colores, teniendo en cuenta que va a pintar todas las regiones y que dos pentágonos son iguales si uno es resultado que girar el otro como los de la figura?
Resultados de la OMM Tamaulipas etapa Municipal 2016
El pasado Viernes 20 de Mayo se realizó la etapa Municipal de la Olimpiada Mexicana de Matemáticas de Tamaulipas. Participaron más de 1200 estudiantes en 12 sedes.
Hasta el momento tenemos las actas con los resultados de 9 de las sedes. Los estudiantes que aparezcan en las listas podrán participar a la siguiente etapa (Etapa Regional) que se tiene programada para el próximo 3 de Junio.
¡Muchas felicidades a los ganadores!
P.D. Estamos en espera de los resultados de Victoria, González y Nuevo Laredo.
Actualización [22 de Mayo a las 14:02]: Ya actualizamos el acta de ganadores de Matamoros.
Resultados de la ONMAPS Tamaulipas 2016
El pasado viernes 14 de Mayo se llevó a cabo la Etapa Final de la Olimpiada Nacional de Matemáticas para Alumnos de Primaria y Secundaria (ONMAPS) de Tamauilpas. El examen se realizó en la Unidad Académica Multidiciplinaria de Ciencias, Educación y Humanidades de la UAT, ubicada en Cd. Victoria, Tamaulipas.
A continuación se enlistan los ganadores que representarán al estado en la etapa Nacional.
Prepárate para el municipal
Como saben, este Viernes 20 de Mayo será la primera etapa en nuestro proceso 2016.
El delegado Orlando ha enviado un examen de prueba para los que quieran conocer que tipo de problemas aparecerán el Viernes, al final lo adjunto.
También aprovecho para recordarles que aún se pueden inscribir para el concurso, llenando el formulario que se encuentra en el siguiente link:
https://docs.google.com/forms/d/1pi8UPeCY2HguynVcoHPfBi_jnmC1UTYvC-ojMYRWjNw/viewform?c=0&w=1
Los esperamos este Viernes :)
Saludos
germán
El nuevo delegado, la convocatoria y los premios.
Acaba de salir la convocatoria oficial (aprobada por la SEP y UAT) para participar en la Olimpiada Mexicana de Matemáticas (OMM) de Tamaulipas. No hay cambios mayores, las fechas, sedes y forma de inscripción son las mismas que ya habíamos mencionado.
Invitamos a todos los interesados a descargar la Convocatoria Oficial y el Cartel para que nos ayuden a difundir este evento que inicia el próximo 20 de Mayo. Los links de descarga los encontrarán al final de esta publicación.

Uno sencillo de conteo
En la siguiente puntícula de $11\times11$ se van a formar triángulos isósceles de tal manera que su lado desigual esté sobre las líneas rosas. ¿Cuántos triángulos isoósceles se pueden formar?
Escalinata
Sea $\triangle ABC$ un trinagulo isósceles con $AC=CB, AB=7$ y altura $CD=9$. Los segmentos $a,b,c,d,e,f,g,h$ e $i$ son paralelos a $AB$ y dividen a $CD$ en $9$ segmentos iguales.
Encuentra $a+b+c+d+e+f+i$
El extraño caso del hexágono azul
En un cuadrado $ABCD$ de lado $60$. $E,F,G$ y $H$ son puntos medios de $AB,BC;CD$ y $DA$, respectivamente. Encuentra el área del hexágono $IJKLMN$.
