Sea n un natural mayor que 2. Supongamos que n islas están ubicadas en un círculo y que entre cada dos islas vecinas hay dos puentes como en la figura:
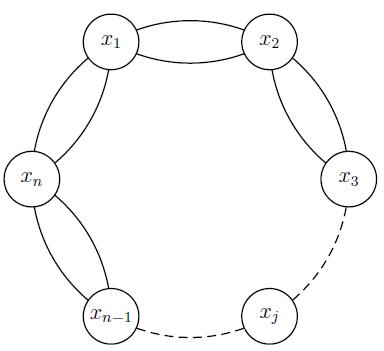
Comenzando en la isla x1, ¿de cuántas maneras se pueden recorrer los 2n puentes pasando por cada puente exactamente una vez?

Sera acaso 2 elevado ala n ??
Sera acaso 2 elevado ala n ??
¿Podrías justificar tu
¿Podrías justificar tu respuesta Casanova?
Pues como son n islas y cada
Pues como son n islas y cada isla desde x1 hasta xn tiene 2 opciones a elegir ( cada puente ), en la segunda vuelta para recorrer todos, solo hay 1 opcion de agarrar ( puesto que de las 2 ya se escojio 1 ) dado esto hay 2 ala n formas de recorrerlos.
Verificando otros casos...
Verificando otros casos... :D
que le parece si lo separo en
que le parece si lo separo en casos... los que van desde
x1-> x2.... xn-1-> xn ->x1 y luego se regresan ( 2 ala n )
x1->xn->xn-1.... x2-> x1 y luego se regresan ( 2 ala n )
ahora solo faltarian las que se empiezan a regresar en x2, x3...., xn-1, xn ( empiezan asia ->)
y las que se empiezan asia el otro lado y empiezan a regresarse en xn, xn-1,....., x2 (empiezan asia <- )
Ok, aqui va, no tube mucho
Ok, aqui va, no tube mucho tiempo ya que acabo de llegar del cellap, pero alparecer el problema 1 y 2 ya salieron. Y ammyo no tengo 2n veamos el por que...
1) Se puede comenzar caminando hacia la isla xn o bien hacia la isla x2
Puesto que ambos casos son simetricos trabajare el segundo, y alfinal agregamos misma cantidad por el primer caso.
2) SI avanzamos de x1 podemos dar vuelta en cualquier isla!!!, por ejemplo, vamos a x2 por alguno de los puentes y regresamos y comenzamos a dar el recorrido en sentido contrario del inicial!!!...(aplicable para cualquier isla....)
3)El problema esta al elegir el primer puente de la ronda, los demas quedan determinados por el puente que se eligio en un principio....
Ahora si, pasemos a resolver el problema....
Comenzamos en la isla y
Comenzamos en la isla x1 y daremos vuelta el la isla xj, (recordemos que en este caso avanzamos como las manecillas del reloj..) hay 2j formas de elegir el camino hacia xj..., el regreso de xj a x1 quedo determinado por los puentes que no elejimos, al regresar a x1, el recorrido ira en contra de las manecillas del reloj, y ya no podemos dar vueltas eso es claro...(por que los puentes entre xj y x1 ya los usamos todos), de ahi de xn hasta xj hay 2n−j formas de hacer el recorrido....de ahi la cantidad de recorridos distintos al dar una vuelta en cada isla seria...
(2j)(2n−j)=2n...ahora, como lo que hicimos es aplicable para cada isla, se tiene que se puede dar vuelta al llegar a la isla x2,x3,...xn,x1 es decir hay 2nn formas de dar el recorrido dando vuelta en una isla, el caso en el que no se da vuelta es en el caso donde se da todo el recorrido como en las manecillas del reloj el cual es equivalente a 2n formas adicionales, de ahi se tiene que hay 2n(n+1) formas de iniciar el recorrido en el sentido de las manecillas del reloj...pero anteriormente mencione que hay la misma cantidad de casos si avanzamos en sentido contrario en un principio...
es decir hay 2(n+1)2n=2n+1(n+1) formas que cumplen las condiciones pedidas...
saludos y espero este correcto y entendible!!
All rait :D
All rait :D
Aaaall right. Esperemos el
Aaaall right. Esperemos el dictamen de Jesús. Pero la solución de Brandon parece no tener ningún hueco.
Muy bien muchachos, sigan así y nos hacemos famosos... bueno yo me apunto por ser el delegado...:)
Los saluda
Muy bien Brandon, yo lo veo
Muy bien Brandon, yo lo veo correcto salvo unos detallitos como 2j en realidad es 2j−1 y no es 2n−j sino 2n−j+1. Pero por lo demás todo está bien.
Saludos
Jesús