Sea T la intersección de la bisectriz de B y la línea media de los lados a y b del triángulo ABC. Vamos a demostrar que P, Q y T están alineados.
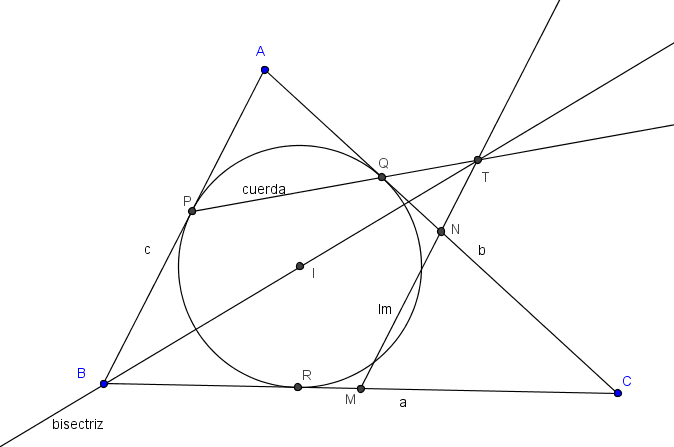
Como se sabe, la línea media MN (de los lados a y b) es paralela a la base c. Viendo la bisectriz de B como transversal a las paralelas AB y MN, se puede ver también que el triángulo ATM es isósceles. Tenemos entonces BM=MT=MC. De aquí que ahora queda de manifiesto que M es centro de un círculo que pasa por B, T y C. Pero BC es diámetro. Se sigue que el triángulo BTC es rectángulo en T.
Por otro lado, el triángulo IQC es rectángulo en Q. Se concluye que el cuadrilátero IQTC es cíclico.
Para demostrar que P, Q y T están alineados vamos a demostrar la igualdad de los ángulos PQA y CQT (con lo cual pasan a ser opuestos por el vértice y la colinealidad queda de manifiesto). Para ello focalicemos el ángulo CIT, el cual es externo en I al triángulo BIC. Es claro entonces que dicho ángulo mide B/2+C/2 (debido a que BI y CI son bisectrices).
Si ahora vemos el isósceles APQ, podemos ver que la bisectriz AI es también mediatriz de PQ. De aquí que el ángulo PQA mide 90-A/2=B/2+C/2. Como se quería.