Problema 1, OMM 2005

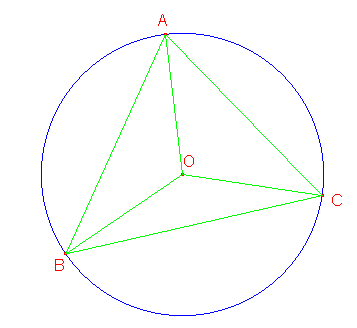
El circuncentro forma isósceles con cada par de vértices del triángulo. Este hecho simple de la geometria del círculo tiene una instancia de uso en este caso para demostrar la semejanza entre los triángulos $ABC$ y $PQR$. Llamemos $\alpha$ a los ángulos en la base $AB$, $\beta$ a los de la base $BC$ y $\gamma$ a los $CA$. Entonces es claro que esos tres ángulos suman 90 grados.

Teniendo a la vista la figura del problema, los ángulos $\beta$ en la base $BC$ son ángulos inscritos en los circuncírculos de $POB$ y de $POC$, con arcos correspondientes a la cuerda común $OP$. Viendo el arco $OP$ desde $R$ se concluye que el ángulo $ORP = \beta$. De manera sililar podemos concluir que el ángulo $OPQ = \beta$.

Por otro lado, $\alpha$ está inscrito en el circuncírculo de $POB$ e intercepta el arco $RO$. Si este arco lo vemos desde $P$, es claro que el ángulo $OPR$ es igual a $\beta$. De manera similar, $\gamma$ intercepta el arco $OQ$ del circuncírculo de $OPC$. Y si vemos $OQ$ desde $P$, se puede ver que el ángulo $OPQ$ es igual a $\gamma$.

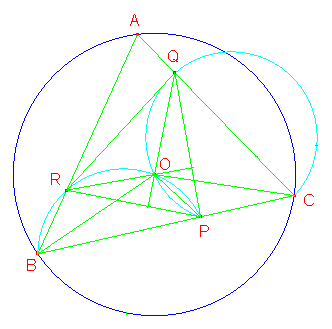
Se concluye entonces que el ángulo $RPQ$ es igual al $CAB$, y que $QO$ es altura (ortogonal a $RP$) del triángulo $PQR$ (puesto que $\alpha$, $\beta$ y $\gamma$ suman 90). Por la misma razón $RO$ es ortogonal a $PQ$.

De aquí que $PO$ sea también ortogonal a $QR$ (las alturas concurren). Pero entonces, los ángulos $QRO$ y $RQO$ son de medidas $\gamma$ y $\alpha$ respectivamente. Se ha demostrado entonces la semejanza de los triángulos $PQR$ y $ABC$, y que $O$ es ortocentro de $PQR$.

Para ver que los triángulos $POB$, $POC$ y $PQR$ son del mismo tamaño, basta observar que cada par de triángulos comparten una cuerda y que ésta, en cada caso, es capaz de un mismo ángulo inscrito en sendos circuncírculos. Si esos ángulos inscritos los trasladamos al centro de sus respectivos círculos se mantienen iguales (aunque su medida se duplica). Se forman entonces dos isósceles congruentes donde los lados iguales son radios.