Publicaciones Recientes
Matemáticas en Tamaulipas
Matemáticas en Tamaulipas es un medio de divulgación de las matemáticas en el estado de Tamaulipas, México. Por lo pronto gira alrededor de las matemáticas de concurso, y en particular de la Olimpiada Mexicana de Matemáticas (OMM), pero aspira a ser sitio Web orientado al mejoramiento de la enseñanza de las matemáticas en el estado.
Reconocimientos
Y después del concurso nacional... ¿felices o felicianos?
Mhhh. Pues la verdad es que nos quedamos lejos de felicianos y muy cerca de ser felices. ¿Por qué? Pues porque nos quedamos en un "casi" de lograr las expectativas con que llegamos a Saltillo el domingo 11 de noviembre.
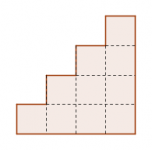
P4 OMM 2006. Zacatecas 2006: n-cubrimiento de una n-escalera
Como se sabe, en problemas de olimpiada, el enunciado puede tener una trampa de significado. El problema 4 del XX concurso nacional de la Olimpiada Mexicana de Matemáticas consiste de una pregunta “para qué enteros…”. La mayoría de los concursantes respondieron a la pregunta. Pero a la hora de las revisiones se supo que no bastaba con decir “estos son” sino que había que demostrar que no había otros. La solución necesitaba estar en el formato “los enteros n cumplen la condición si, y sólo si, son de la forma n = f(k)”. He aquí el enunciado del problema 4 del concurso nacional de 2006.
Un teorema sobre primos
Para todo primo $ p $, si $p^2 + 2$ es primo entonces $p^3 + 2$ es también primo.
Ternas Pitagóricas
Demuestre que para cualquier terna pitagórica $a^2+b^2=c^2$, alguno de los números $a, b, c$ es divisible por tres.
Sucesión Aritmética y prueba de coprimalidad
Si ninguno de los números $b,2b,...,(m-1)b$ es divisible entre $m$, entonces $m$ y $b$ son coprimos.
Un problema interesante de exponentes
Problema. Encontrar todos los enteros positivos $a,b$ tales que $a^b=b^a$
Monterrey 97
Como se sabe, uno de los 6 problemas del concurso nacional de la Olimpiada Mexicana de Matemáticas es trivial –por lo menos para quienes han tenido un buen entrenamiento. He aquí el enunciado del primer problema del concurso nacional de 1997.
Encuentra todos los números primos positivos p tales que también sea un primo positivo.
XX Avanzados
Encuentra todas las parejas de números $(a,b)$ tales que $a-b$ es un número primo y el producto $ ab$ es un cuadrado perfecto.
