Publicaciones Recientes
Calendario de entrenamientos y un takehome-selectivo
Los siguientes 4 entrenamientos se llevarán a cabo en las instalaciones de la UAMCEH-UAT en Cd Victoria y se apegarán al formato de viernes en la tarde, sábado todo el día , y domingo en la mañana. Se usará el Engel para cubrir las estrategias básicas de solución de problemas (traer para copias).
La IX Olimpiada Norestense de Matemáticas manchada por el problema 2
Dando la bienvenida a una propuesta hecha por Hector Flores Cantú --entrenador y casi delegado de Nuevo León-- a Jesús Rodríguez Viorato (entrenador y padrino de esta delegación, y web master de MaTeTaM), la delegación Tamaulipas decidió elaborar un examen inédito para la IX Olimpiada Norestense de Matemáticas, celebrada este fin de semana en las instalaciones de la UAMCEH-UAT y financiada en sus gastos por el gobierno del estado de Tamaulipas (quien pagó hospedaje.y alimentación de 54 personas por tres días y 2 noches en el RAMADA de Cd Victoria).
IX Olimpiada Norestense de Matemáticas (Problema 3)
El incírculo del triángulo $\triangle ABC$ es tangente al lado $AB$ en el punto $P$ y al lado $ BC $ en el punto $Q$. El círculo que pasa por los puntos $A,P,Q$ corta por segunda vez a la recta $ BC $ en $ M $ y el círculo que pasa por los puntos $C,P,Q$ corta por segunda vez a la recta $ AB $ en el punto $ N $.
Eliminación con dos operaciones
En cada cuadrado de un tablero rectangular hay un entero positivo. Se pueden modificar los números del tablero usando alguno de los siguientes movimientos.
--Multiplicar por 2 cada número de un renglón.
--Restar 1 a cada número de una columna.
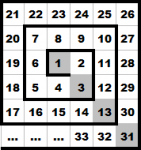
Números en espiral
Considera la sucesión $\{1,3,13,31,\ldots\}$ que se obtiene al seguir en diagonal el siguiente arreglo de números en espiral.
Encuentra el número en la posición 100 de esa sucesión.
IX Olimpiada Norestense de Matemáticas
Cd Victoria, Tamaulipas
UAMCEH-UAT
a 29 de septiembre de 2009
La Delegación Tamaulipas de la XXIII Olimpiada Mexicana de Matemáticas, informa a las delegaciones de Coahuila, Nuevo León y Tamaulipas, sobre el programa de actividades de la IX Olimpiada Norestense de Matemáticas, con sede en la Unidad Académica Multidisciplinaria de Ciencias, Educación y Humanidades de la Universidad Autónoma de Tamaulipas (UAMCEH-UAT) en Ciudad Victoria.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 6)
Alrededor de una circunferencia se marcan 6000 puntos y cada uno se colorea con uno de 10 colores dados, de manera tal que entre cualesquiera 100 puntos consecutivos siempre figuran los 10 colores. Hallar el menor valor k con la siguiente propiedad: Para toda coloración de este tipo existen $k $ puntos consecutivos entre los cuales figuran los 10 colores.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 5)
La sucesión $a_n$ está definida por
$a_1=1, a_{2k}=1+a_k$ y $a_{2k+1}=\frac{1}{a_{2k}}$, para todo entero $k\geq 1$.
Demostrar que todo número racional positivo aparece exactamente una vez en esa sucesión.
XXIV Olimpiada Iberoamericana de Matemáticas (problema 4)
Sea $ ABC $ un triángulo con $AB\neq AC$. Sean $ I $ el incentro de $ ABC $ y $ P $ el otro punto de intersección de la bisectriz exterior del ángulo $A $ con el circuncírculo de $ ABC $. La recta $PI$ intersecta por segunda vez al circuncírculo de $ ABC $ en el punto $J $. Demostrar que los circuncírculos de los triángulos $JIB$ y $JIC$ son tangentes a $IC$ y a $IB$, respectivamente.
Olimpiada Iberoamericana de Matemáticas 2009
Hoy inició la XXIV Olimpiada Iberoamericana de Matemáticas en la Ciudad de Querétaro, México. Es decir, hoy los adolescentes aspirantes a una medalla presentaron la primera parte del examen, consistente en tres problemas. Mañana presentan los siguientes tres, con lo cual la suerte estará echada...

