En este post quiero presentar una solución del último problema de la norestense que casi me convence. Invito a los lectores de MaTeTaM a encontrar el error y comentarnos sus impresiones. Y claro, también, si tienen una solución al problema no duden en compartirla.
Bueno, el enunciado del problema es el siguiente.
En un grupo de personas, cada dos de ellas tiene exactamente un amigo en común en el grupo. Prueba que hay una persona que es amiga de todas las demás personas en el grupo. (Nota: la amistad es mutua, es decir, si X es amigo de Y, entonces Y es amigo de X.)
La solución errónea.
Procederemos por contradicción: supongamos que se cumple la condición, pero no hay ninguna persona que sea amigo de todos. Luego, consideremos una persona x con la mayor cantidad de amigos (esto es, no hay otra persona que tenga más amigos que x).
Entonces, debe existir al menos una persona y en el grupo que no es amigo de x. Trataremos ahora de llegar a una contradicción sobre la existencia de y.
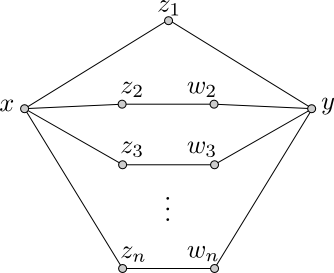
Por la hipótesis del problema x y y deben tener un único amigo en común, llamésmoslo z1. Ahora bien, llamemos z2,z3,⋯zn al resto de los amigos de x.
El siguiente diagrama ilustra la notación.

Para cada zi con i>1 sabemos que y y zi deben tener un único amigo en común. Llamemos a ese amigo wi, para i=2,3,…,n. Entonces, cada uno de los wi's son distintos. Pues si wi=wj, con i≠j, entonces zi y zj tendrían a wi como amigo común. Pero ya tenían a x. Esto contradice la unicidad de los amigos.
Ahora bien, cada uno de los wi's es vecino de y. De aquí que w2,w3,…,wn son (n−1) vecinos de y, más z1 nos da como resultado que y tiene al menos la misma cantidad de amigos que x.
Por último, z1 y y deben tener un amigo común, llamésmoslos p. Pero al igual que antes, p no puede ser igual a un wi pues de lo contrario (si wi=p para algún i), z1 y zi tendría más de un amigo común, a saber, x y wi=p.
Pero esto significa que y tiene más amigos que x. Una contradicción a la condicción inicial con la que se eligió x (nadie tiene más amigos que x). La figura final de la contradicción es la que sigue:

Espero que les halla gustado esta "demostración" y que más les guste buscarle el error.
Saludos

Hace algunos días, lunes para
Hace algunos días, lunes para ser exacto, intenté resolver éste problema, aunque solo vi el enunciado y no la situación que lo envolvía. Mientras lo resolvía iba por el mismo camino de ésta solucón, no obstante no pude avanzar más debido a que no consíderé a la persona "x", como ingeniosamente se hace en esta demostración, como la persona que posee la mayor cantidad de amigos. Debido a esto empezé pensar en otros caminos para demostrarlo, y me di cuenta que la afirmación "hay una persona que es amiga de todas las demás personas en el grupo" es falsa cuando el grupo de personas es par. Esto fue lo que visualizé:
Supongamos que la afirmación del problema es correcta y que la cantidad de personas en el grupo es par.
Sea x la persona que es amiga de todas las demás. Por la condición inicial del problema la cantidad de amigos que tiene es impar, sean z1,z2,...,z(2n+1) sus amigos.
Para cada zi y x se cumple que el amigo que tienen en común es un zj, para i≠j, y debido a que cuales quiera 2 personas del grupo solo tienen un amigo en común, zi es el amigo que tienen en común x y zj. ya que de lo contrario x y zj tendrían 2 amigos en común, de aqui que cada zi del conjunto solo tiene 2 amigos, zj y x, y debido a que el número de amigos de x es impar existirá una persona zk que no tendrá un amigo en común con x, estableciendo una contradicción.
Me gustaría que verificaran este razonamiento en caso de que haya pasado por alto algo y, en realidad la paridad del conjunto no sea un problema.
Cuando me dí cuenta de la contradicción anterior decidí volver a leer el problema, pensando que era posible que lo hubiera leido incorrectamente, pero no fue así, y me percaté de la controversia que se había sucitado debido a éste. No se me ha ocurrido una solución, pero me parece que el error de la "solución" establecida por jesús podría estar en el hecho implícito de que cada wi no puede ser amigo de x, ya que eso implicaría que existen dos amigos de x que poseen como otro amigo en común, y.
Hace tiempo que no sabíamos
Hace tiempo que no sabíamos de ti en Matetam. Un gusto leerte de nuevo y ver que aun sigues razonando de forma tan clara y perfecta. Sin mencionar que tu estilo de redacción ha mejorado muchísimo.
Bueno, sobre tu post, tu demostración es correcta. Has demostrado que el número de vértices de la gráfica no puede ser par, es decir, tiene que se impar. Incluso, creo que tus argumentos se pueden reusar para demostrar que toda persona en un grupo de éstos, tiene que conocer a un número par de personas.
Por último, no entendí esta frase:
No le entiendo bien, tal vez te equivocaste en las letras. No se si puedas explicarme más, pues ciertamente cada wi no es amigo de x.
Hola Jesus... pues como ves
Hola Jesus... pues como ves de nuevo la embarramos en el examen norestense... la que mencionas aquí es en esencia la idea (incorrecta) de la solución que nos presentaron en la norestense...
En tu solución me parece que no justificas que los wi sean diferentes a z1.
Saludos
Hola Hector... pues sí,
Hola Hector... pues sí, efectivamente el error está en no justificar que los wi's sean diferentes a z1. Ya que en realidad uno de los wi's tiene que ser igual a z1, de ahí se desprende que en el conteo final sale uno de más.
Por otro lado, la verdad es que es fácil equivocarse en estas cosas y, más aún con el tiempo tan corto para estudiar los problemas y las soluciones propuestas.
Saludos