Didácticos

Una preguntar muy común en matemáticas de concurso y escolares es la siguiente:

¿Cuál es el área rectangular más grande que se puede cubrir con un cerca de 500 metros de longitud?

Probablemente esté más comúnmente en cursos de precálculo o de de calculo diferencial I. Pero también puede aparecer en cursos de álgebra. La técnica que veremos aquí, es para aquellos que quieren resolverlo usando sólo álgebra (con muy poco conocimiento de desigualdades).

Las técnica podría presentarse a estudiantes de secundaria interesados en Matemáticas de Concurso. Pues es fácil de presentar si ya saben álgebra.

Una de las primeras propiedades que se presentan cuando aprendemos divisibilidad es la siguiente: 

Si $d$ es divisor de $a$ y $b$, entonces $ d | ax + by$ para cualesquiera enteros $x,y$.

A menos que se diga lo contrario, supondremos que estamos usando enteros mayores a cero. La propiedad citada lo que nos dice es que, si $d$ es un divisor común de $a$ y $b$ entonces $d$ es divisor de cualquier combinación lineal de ellos. Hemos hablado de dos conceptos muy importantes de los que se profundizará más.

El problema

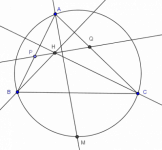
Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.

La solución

De acuerdo a los datos sobre la recta PQ que pasa por H, es fácil darse cuenta que PQ es bisectriz de los ángulos formados en H por las alturas.

En el presente post voy a presentar la solución de un problema de números que se me hizo realmente difícil y no lo pude resolver sin ayuda. Trato también de trasmitir a los lectores de MaTeTaM el modo de razonar de un experto en el problem solving de concurso. El problema es el siguiente:

Demostrar que, para todo entero no negativo k, $$2^{2^{6k+2}}+3$$ es múltiplo de 19.

Demostración (reconstruida a partir de una realizada por JRV en conversación telefónica con el que esto escribe)

Creo que puede ser de alguna utilidad para los lectores de MaTeTaM la discusión de dos demostraciones del conocido teorema que dice:

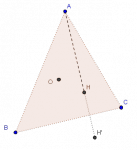
El reflejo del ortocentro en el espejo de cualquier lado del triángulo pertenece al circuncírculo.

Una de ellas procede reflejando $H$ en un lado (digamos $BC$) y demuestra que ese reflejo (digamos $H'$) pertenece al circuncírculo; la otra toma el punto $H'$ de intersección de la altura (digamos $AH$) con el circuncírculo y demuestra que $H'$ es el reflejo de $H$ (en $BC$).

Es bastante inusual que un problema de matemáticas de concurso llegue a la prensa diaria. Por ello es que me sorprendió que haya aparecido en El Universal el siguiente problema de matemáticas (aunque más bien es de lógica) en estos días de abril de 2015. (La nota decía, además, que el problema es de una olimpiada de Singapur --creo-- para niños de 14 años y se había vuelto viral en la WWW.)

Me he encontrado en estos días con la notabilísima identidad algebraica (para a,b,c reales):
$$abc+(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)$$
Su rasgo distintivo radica --creo-- en que el lado derecho refleja el izquierdo pero intercambiando la suma por el producto y éste por aquélla. Es decir, lo que en el lado izquierdo es producto en el derecho es suma y la suma en el izquierdo es producto en el derecho.

Ahora que el 2014 se ha quedado atrás y el puente Guadalupe Reyes se terminó es buen momento para mirar hacia el futuro. Y desearle a toda la comunidad de usuarios de MaTeTaM un 2015 de eficaces aprendizajes en el problem solving de matemáticas.

Y, bueno, de paso voy a plantear la tesis de que, en el aprendizaje de las matemáticas, primero se aprende el procedimiento y sólo después de ello se aprende el concepto. Ilustro con un ejemplo de desigualdades.

Voy a presentar en este post una forma de demostrar la desigualdad de Titu Andreescu que recuerda los procesos de bootstraping utilizados en computación --y otras áreas de la ciencia. El término bootstrapping está inspirado --verosímilmente-- en Las Sorprendentes Aventuras del Baron de Munchausen. (Una serie de narraciones donde el héroe realiza tareas imposibles.) Atacho una traducción al español.

El problema y la solución de Germán