Didácticos
¿Combinatoria biyectiva? OK, pero ¿cómo descubres la biyección?
Regresemos al problema del post anterior (subconjuntos sin consecutivos):
Sea S={1,2,...,n}. ¿De cuántas formas se puede elegir un subconjunto de tamaño r y sin consecutivos?
Solución biyectiva ("descubierta" con el método regula falsi)
Sin restricciones serían C(n,r). Pero algunos de esos subconjuntos tienen consecutivos. Sea B={b1,b2,...,br} un subconjunto de S de tamaño r. Por ejemplo, si fuese B={1,2,...,r}, lo podríamos convertir a {1,3,5,...} --que no tiene consecutivos--, lo cual equivale a dejar el primero igual, sumarle 1 al segundo, 2 al tercero, etc.Regresemos al problema del post anterior (subconjuntos sin consecutivos):
Sea S={1,2,...,n}. ¿De cuántas formas se puede elegir un subconjunto de tamaño r y sin consecutivos?
Beneficios y costos de la abstracción matemática
Se tienen 7 bolas blancas y 5 negras. ¿De cuántas formas se pueden colocar las 12 en hilera sin que haya dos negras juntas?
Solución
Coloco las 5 negras. Utilizo 4 blancas para separarlas. Me quedan 3 blancas. ¿Dónde las pongo? Es decir ¿cuántas formas hay de colocarlas en la hilera de las ya colocadas? Este problema es difícil a pesar de su aparente simplicidad. Una forma de responder a la pregunta es separar en casos: coloco las tres en lugares diferentes, coloco dos juntas en un lugar y la otra en otro lugar y, finalmente, las coloco las tres en un solo lugar.
Un ejercicio de prueba biyectiva en combinatoria
Como se sabe, el número de elementos del producto cartesiano de dos conjuntos finitos es el producto de las cardinalidades de los conjuntos. Pero aquí vamos a exhibir una demostración de ese hecho aplicando una prueba biyectiva de |A×B|=|A||B|.
Para demostrarlo vamos a definir una función entre el producto cartesiano A×B y el conjunto de enteros S={0,1,...,|A||B|−1}.
Arco capaz: un problema de lugar geométrico
En este post voy a definir el problema de lugar geométrico denominado arco capaz y a discutir el procedimiento de su construcción.
El problema y su procedimiento de construcción
En el problema de lugar geométrico denominado arco capaz, se da un segmento AB y un ángulo λ. Se pide describir el lugar geométrico de los puntos en el plano, desde los que el segmento AB se ve desde un ángulo λ.
Para quienes tienen prisa, el procedimiento de construcción es el siguiente:
Invariantes: un frame que permite razonar por el absurdo
Invariantes
(Adaptado de http://boumbo.toonywood.org/xavier/old/maths/stmalo/base-cours.pdf )
Se tiene un conjunto de configuraciones (por ejemplo, estados o posiciones en un juego). A una configuración inicial se le aplica una transformación (una jugada) sujeta a ciertas reglas (las reglas del juego) y sobre la configuración resultante se aplica otra transformación de acuerdo a las mismas reglas (el juego sigue). Se pide decidir si una cierta configuración puede o no obtenerse mediante transformaciones válidas partiendo de una configuración inicial.
Álgebra como lenguaje (a propósito del problema de álgebra)
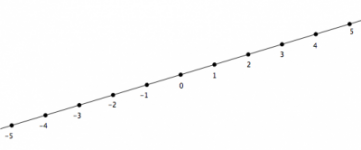
Segmentos Dirigidos
Este concepto se oye mucho en las Olimpiadas de Matemáticas, pero --como muchos otros de olimpiada-- no es un tema que se enseñe en bachillerato. Esto puede llegar a asustar a muchos estudiantes, pero en realidad es un tema al que nada hay que temerle. Es muy fácil de entender y sobre todo es muy útil.
La idea principal de los segmento dirigidos es agregar una propiedad extra a la noción de segmento. Esta propiedad se resume así:
Estos eran dos amigos...
B: Ah…Mmhh… Creo que esa sí me la sé. Es base por altura. ¿Cierto?
A: ¿Pero si no te dan la altura?
B: Bueno, pues ¿qué te dan?
A: Te dan las longitudes de los lados.
B: Bueno, entonces saco la altura con el seno del ángulo ¿te dan un ángulo?
A: No.
B: Ah pues deja ver…Creo que se puede eliminar el seno utilizando la ley de cosenos… eso lo hice una vez cuando estudié la secundaria… Deja ver si me sale…
2(ABC)=ah=absenC ¿OK?
A: Con (ABC) estás denotando el área del triángulo ABC ¿no es así?

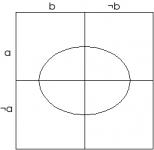
Diagrama de Lewis Carroll