Geometría
La poderosa Todotriz.
Antes de empezar a leer este blog, se deben de conocer los conceptos de Bisectriz, Mediatriz, Mediana y Altura de un triangulo.
Este tema la verdad es muy sencillo, pero puede llegar a ser muy util tanto para novatos como para experimentados. Veamos de que trata.
Sea ABC un triangulo con AB=AC. Si trazamos la perpendicular a BC desde A, esa recta sera mediatriz, bisectriz, mediana y altura. Es todo!! (o bueno no se si literalmente todo), entonces, podriamos decir que es una Todotriz. Este es un quintuple si y solo si, y la demostracion es trivial.
CARMA y su geometria troll
Antes de hablar del punto fantasma (no tengo acceso a una computadora entonces quiero hablar de algo simple xD), hace unos dias estaba entrenando para la CVM de CARMA porque es la primera a la que le voy a entrar, y el P4 de 2021 lo senti de que "que es esto?", y en si, todos los problemas de geo de CARMA para mi son muy trolls, o sea, no dificiles, pero tienes que ver algo que mate sus problemas (nome gusta eso xD). Pero bueno, veamos lo que hay.
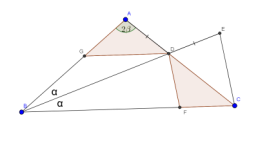
Sea ABC un triángulo con AB = 15 cm y BC = 20 cm. Considera la circunferencia que pasa por los tres vértices del triángulo. Si la tangente a dicha circunferencia en B es perpendicular a la recta que contiene el segmento AC. Determina la medida del segmento AC en centimetros.
Actividad de Verano para Preselección Tamaulipas 2016 (Jornada 1)
El día de hoy comenzamos con las actividades para la preparación de la Preselección Tamaulipas 2016 en el receso de verano.
Para esto diseñamos un juego al estilo de las Ligas Fantásticas deportivas que hay para varios deportes. Adjunto el archivo con las reglas del juego.
Cada semana serán equipos distintos, y podríamos ajustar algunas reglas para hacer más interesante la actividad. Semana a semana se irá actualizando el ranking de la puntuación obtenida por cada alumno.
Prepárate para el Estatal con MaTeTaM (Geometria)
Siguiendo con esta serie de posts dejaré los temas importantes para el estatal, en este caso para geometria. También una lista de problemas (listageometria2016) y algunos entrenamientos, se da por sentado el tema de áreas, la lista incluye unos pocos problemas de esto pero son retadores.
No es cien por ciento necesario que aprendan a hacer demostraciones aún pero algunos problemas de geometria solo se pueden aprender si se conocen las demostraciones de algunos resultados y en que instancias se usan.
1. Ángulos entre paralelas. Hacer problemas del entrenamiento adjunto.
Sobre el problema 1 de la 29 OMM
El problema
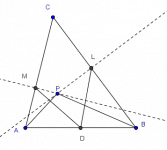
Sea ABC un triángulo y sea H su ortocentro. Sea PQ un segmento que pasa por H con P en AB, Q en AC y tal que ∠PHB=∠CHQ. Finalmente en el ciruncírculo del triángulo ABC considera M el punto medio del arco BC que no contiene a A. Muestra que MP=MQ.
La solución
De acuerdo a los datos sobre la recta PQ que pasa por H, es fácil darse cuenta que PQ es bisectriz de los ángulos formados en H por las alturas.
Sobre el ortocentro reflejado y el problema 3G
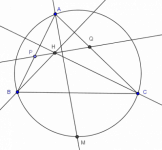
Creo que puede ser de alguna utilidad para los lectores de MaTeTaM la discusión de dos demostraciones del conocido teorema que dice:
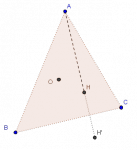
El reflejo del ortocentro en el espejo de cualquier lado del triángulo pertenece al circuncírculo.
Una de ellas procede reflejando H en un lado (digamos BC) y demuestra que ese reflejo (digamos H′) pertenece al circuncírculo; la otra toma el punto H′ de intersección de la altura (digamos AH) con el circuncírculo y demuestra que H′ es el reflejo de H (en BC).
Cuadrilátero cíclico: más instancias de uso
En este post voy a recomendar el estudio de algunos materiales sobre cuadriláteros cíclicos a quienes se están preparando para el nacional. De paso intercalo dos instancias de su uso.
En un post anterior --dedicado a los criterios de reconocimiento de los cuadriláteros cíclicos-- hemos destacado la importancia de esta herramienta en el problem solving de geometría y discutimos varias instancias de uso asociadas a demostraciones del teorema de la mariposa.
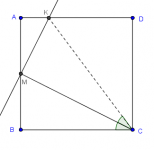
Héctor R. Flores C.: una didáctica del reconocimiento
Cuadrilátero cíclico --criterios e instancias de uso
Puesto que el material disponible en la Web sobre los cuadriláteros cíclicos no incluye las demostraciones de los criterios de su reconocimiento (con excepciones difíciles de encontrar) voy a presentar en este post los tres criterios para el reconocimiento de un cuadrilátero cíclico, así como sus demostraciones. Añado tres instancias de uso.
Definición y criterios de reconocimiento
Primero la definición:
Si los cuatro vértices de un cuadrilátero convexo están sobre la misma circunferencia, entonces se dice que el cuadrilátero es cíclico.
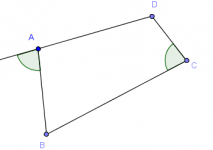
El difícil de la ONMAPS --Tamaulipas 2014