Es una variante del diagrama de Venn-Euler que facilita la clasificación de un universo Sde objetos según tres atributos a, b y c. La clasificación es dicotómica: cada objeto de S ya sea tiene la propiedad o atributo a, b, o c o bien no la tiene (esto último se representa con ¬a, ¬b, o ¬c).
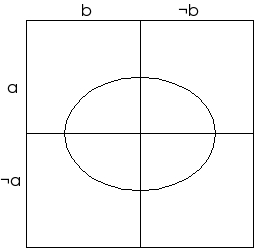
Cada región del diagrama representa un subconjunto de los objetos con tres propiedades (si incluimos los atributos complementarios ¬a, ¬b y ¬c como atributos).
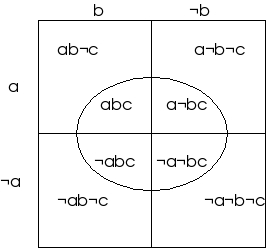
Ejemplo 1
Universo de objetos = los libros de la biblioteca
| Atributos considerados | Datos del acertijo |
|---|---|
| a = presentación rústica = R | - 34 encuadernados de los cuales 3 son de historia en francés. |
| ¬a = presentación encuadernada = ¬R = E | - 52 de historia de los cuales 27 están en inglés. |
| b = (tema) historia = H | - 46 en inglés, la mitad en rústica. |
| ¬b = (tema) literatura = ¬H = L | - 20 de literatura en francés. |
| c = (idioma) francés = F | - 31 en rústica de literatura. |
| ¬c = (idioma) inglés = ¬F = I |
Clasificar todos los libros de acuerdo a los tres criterios (tema, idioma, encuadernado)
Solución

Los datos se escriben en la frontera entre un atributo y su complementario cuando no se sabe (no se menciona en el enunciado) cómo se reparten los objetos entre esas dos propiedades complementarias. Ejemplo: 27 de historia en inglés se interpreta como 1) en el primer renglón, 2) fuera del círculo, pero 3) se desconoce cuántos de ellos están en rústica y cuántos están en encuadernados.
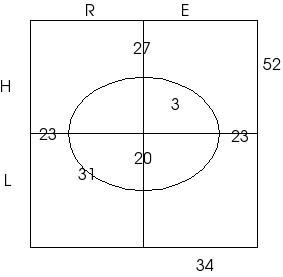
La forma en que se va llenando el diagrama de Lewis Carroll se ilustra con diagramas sucesivos (mostrados a continuación) acompañados de una explicación de la forma en que se realiza la deducción de nuevos datos a partir de los ya conocidos hasta el momento.
Se trata de un llenado en cámara lenta. Con la práctica tal proceso de llenado puede llegar a realizarse muy rápido y sobre un mismo diagrama.
| Figura | Explicación | Comentario |
|---|---|---|
 |
Como hay 34 E y 23 de ellos en I entonces debe haber 11 encuadernados en F. Pero hay 3 E de H en F. Por tanto, debe haber 8 encuadernados de literatura en francés. (No se incluyen los números ya en el primero para no recargar la figura) | Nótese que todos los datos están en el diagrama inicial. No es necesario ir a verlos en el enunciado del problema. Después de saber leer el diagrama el proceso de deducciones sucesivas y llenados se agiliza en extremo. |
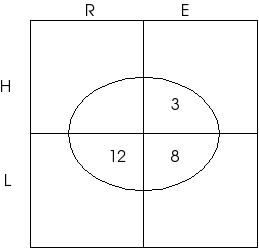 |
Como hay 20 de L en F (en la frontera entre R y E en el diagrama inicial) y 8 E (añadido en 2o. diagrama) entonces 12 deben estar en R | La deducción es elemental. 20LF=8LFE+?LFR |
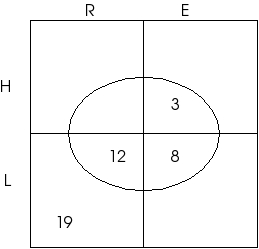 |
Como hay 12 LRF y 31 LR entonces debe haber 19 LRI | En palabras, * hay 12 libros de literatura en rústico en francés, * 31 son de literatura en rústico en inglés |
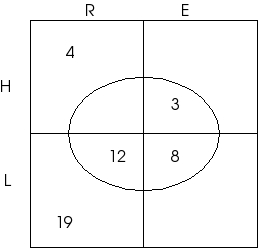 |
Como hay 23 RI y 19 RLI entonces debe haber 4 RHI | De aquí en adelante las deducciones se desgranan. Todas son de complementación. |
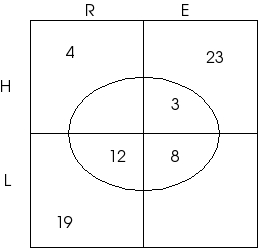 |
Como hay 27 HI y 4 HRI entonces debe haber 23 HEI | Por complementación, es decir, si un conjunto tiene 27 elementos y una de sus partes tiene 4 entonces la otra tiene 23. |
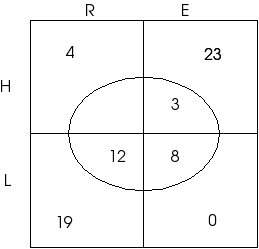 |
Como hay 23 EI y 23 HEI entonces debe haber 0 LEI | Si un conjunto tiene dos partes y una de ellas contiene todos los elementos entonces la otra no tiene elementos |
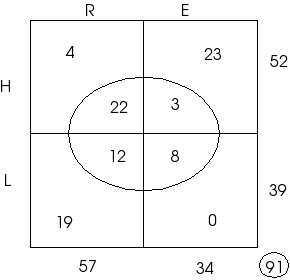 |
Como hay 52H y 4HRI + 23HEI + 3HEF = 30 entonces debe haber 22 = 52 - 30 de HRF | Si un conjunto tiene 4 partes y se sabe que tres de ellas … |
