Septiembre 2013
Teorema fundamental de la proporcionalidad (Tales)
Si una recta paralela al lado BC del triángulo ABC corta en B′ a AB y en C′ a AC), entonces ABAB′=ACAC′=BCB′C′
Este es el Teorema de Tales para triángulos del cual hemos hablado ya en MaTeTaM. En esta oportunidad comentaré el teorema particularizado para triángulos rectángulos y lo demostraré con el método de áreas.
El 5 del VI concurso nacional OMM 1992
Cuando llueve, como en estos días que se formó en el Golfo de México la tormenta Ingrid, me pongo inspirado y con ganas de postear. Buscando qué hacer mientras llovía me encontré con este problema del concurso nacional de 1992 (VI OMM).
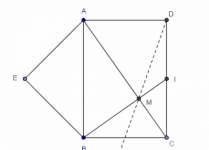
Un problema de geometría --de Wong Yan Loi
En su libro Introduction to geometry, Wong Yan Loi presenta el problema motivo de este post (y lo resuelve con geometría analítica). La redacción del enunciado está aquí ligeramente modificada y a la solución le he añadido explicaciones que Wong Yan Loi se ahorra. (Me gustaría ver una solución sintética de este problema. Si alguien la encuentra sería una buena obra que la compartiera con los lectores de MaTeTaM.)
Entrenamiento en Olimpiada --de Orlando Ochoa
Orlando Ochoa Castillo generosamente ha enviado a la Delegación Tamaulipas de la OMM el contenido de los entrenamientos de la selección Guanajuato. No los había puesto en MaTeTaM porque no sabía cómo --dado que están en formato PDF.
Los comparto ahora con los lectores de MaTeTaM (como es la intención expresa de Orlando) para que estén disponibles en la Web para quien quiera seguirlos por su cuenta y, en particular, para los (futuros) preseleccionados de Tamaulipas --para la segunda semana de octubre se definirán. El material --que incluyo en los atachados-- consiste de nueve sesiones y algunas tareas.
