Didácticos
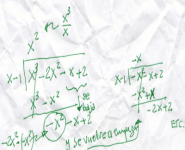
Cinco problemas equivalentes al de Fibonacci
Voy a plantear en este post cinco problemas de combinatoria que son equivalentes al problema de los conejos de Fibonacci, en el sentido de que dan lugar a la misma sucesión (y a la misma recurrencia). La solución de cada uno de ellos se detiene en el modelo, es decir, en el razonamiento por recurrencia que conduce a plantearlo.
1. Subconjuntos sin consecutivos
¿De cuántas formas se puede elegir un subconjunto de {1,2,…,n} de manera que no contenga números consecutivos?
Solución
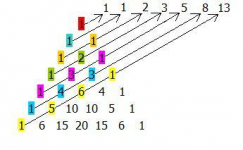
Sucesiones, recursividad y diferencias finitas
En este post voy a abordar de nuevo el tema de la recursividad a través de algunas sucesiones definidas de manera recursiva. Puesto que la recursión es un tipo de razonamiento muy útil en el problem solving de combinatoria, voy a plantear primero algunos ejemplos de modelación, un tema que se omite en la mayoría de los textos sobre el tema.

El misterioso hechizo del problem solving
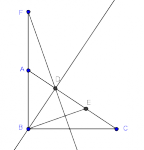
En días pasados subí a MaTeTaM todos los problemas de la ONMAS que pude encontrar, y hubo uno que ya había publicado en 2010 y que llamó mi atención pues se ve bastante difícil... y más difícil es la solución que envió Brandon en su momento (basada en una semejanza).
Bueno, lo difícil es entender la demostración que da de la semejanza --yo no le entendí. El caso es que lo traje en al cabeza varios días, lo resolví de otra manera (por ortocentro) y generé un problema parecido... pero no podía demostrar la semejanza (que parecía obvia en la figura) de una manera alternativa a la que dio Brandon.
Kevin: talento matemático infantil --en la periferia
Hablando de la educación matemática en USA, un matemático americano desencantado decía: lo verdaderamente extraordinario es encontrar un niño que resuelva problemas de rutina con métodos de rutina. (Ver la segunda postdata de mi post sobre la división larga.)
Hay pocas cosas que le alegran el día a un profesor de matemáticas desencantado de la educación. Una de ellas es encontrar o descubrir un niño con aquellas habilidades matemáticas que solían ser las obligatorias.
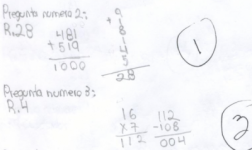
Ranas, hormigas, camaleones...
Después de escribir el post sobre paridad estuve navegando la Web con el tema invariantes, otro tipo de razonamiento en el problem solving de olimpiada que generalmente acompaña al de paridad.

Argumento de paridad: tres instancias de uso
Voy a discutir en este post un razonamiento elemental en el campo de las matemáticas de concurso denominado argumento de paridad. Es recurrente en el problem solving de olimpiada. Se presentan las propiedades básicas de la paridad y algunas instancias de uso.
Discusión previa
Así como las personas pueden ser clasificados por su sexo (femenino/masculino), los números enteros se pueden clasificar por su paridad (par, impar).
La paridad de un entero es así una variable dicotómica: el número es par o bien no lo es (en cuyo caso se le llama impar o non). Una clasificación elemental... pero tiene sus detalles finos (esa verdad no está en los libros, sino en sus instancias de uso).
Una propiedad elemental de la divisibilidad
Voy a discutir en este post una propiedad de la divisibilidad que surge cuando la suma de dos números es múltiplo de un primo. Se le podría llamar propiedad de transferencia de la divisibilidad. Incluyo dos instancias de uso en el problem solving de olimpiada.
Una propiedad de transferencia
Considere la suma a+b de dos números enteros y supongamos que es múltiplo de un primo p. Puede suceder que ninguno de los sumandos sea múltiplo de p. Pero si alguno lo es, entonces también lo es el otro. Formalmente, la propiedad se puede establecer así:
a,b∈Z,p primo, p|a+b⇒(p|a⇔p|b)
Principio de sustitución
Si dos cantidades son iguales entonces son intercambiables --en el cálculo o demostración.
Parece trivial. Y lo es. Pero hay que aprender a usarlo. Antiguamente se solía decir:
Dos cosas iguales a una tercera son iguales entre sí.
Pero no se trata de aprender a recitarlo, se trata de aprender a usarlo.
Ejemplos:
1. Considere el sistema x+y=z, z=5
Aquí tenemos que (dos cosas) x+y y 5 son iguales a z (una tercera). Por tanto, x+y=5 (son iguales entre sí).
Discusión sobre las coordenadas de un punto
División sintética --cálculo numérico de P(x)/(x−c)