Didácticos
Método Singapur --para razonar problemas verbales elementales
Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con
Un ejemplo
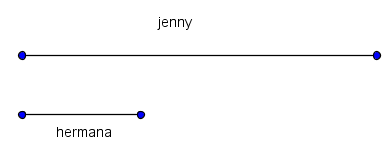
Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?
Solución algebraica
El fácil del concurso XV OMM (2001)
Con motivo del comentario-solución de Germán Puga Castillo al problema 1 del concurso nacional de la OMM 2001 (y el feedback de Jesús Rodríguez Viorato), el problema llamó mi atención por su aparente simplicidad. Voy a comentarlo en este post (y a resolverlo apoyándome en la idea de Germán). El problema es el siguiente:
Encuentra todos los números de 7 dígitos que son múltiplos de 3 y de 7, y cada uno de cuyos dígitos es 3 o 7.
Dos problemas razonados --para segundo de secundaria
En este post voy a discutir dos problemas razonados que, según la reforma de secundarias 2011, los alumnos que pasan a tercer año deberían estar en posibilidad de resolverlos. Su modelación conduce a un sistema 2×2 (dos ecuaciones, dos incógnitas).
Idealmente están al alcance de un adolescente de 14, pues en el bloque V del programa de matemáticas de segundo de secundaria, uno de los aprendizajes esperados es:
Resuelve problemas que implican el uso de sistemas de dos ecuaciones lineales con dos incógnitas.
Análisis de algunos problemas ENLACE 2012
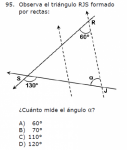
Cuatro problemas elementales de aritmética
En los entrenamientos de la selección ONMAS Tamaulipas 2013 me tocaron 2 sesiones de 3 horas cada una. De ahí elegí 4 problemas de aritmética para presentarlos en este post, en el cual voy a resolverlos y a comentarlos.
A pesar de ser elementales, están lejos de ser triviales. Digo, considerando que fueron para alumnos de primaria y secundaria. (Para el alumno promedio muy probablemente cada uno de ellos es un proyecto de investigación.)
ONMAS Tamaulipas 2013: los problemas y algunas soluciones
En este post voy a presentar los problemas del concurso ONMAS Tamaulipas 2013 y a comentar algunos de ellos.
Los problemas
Concurso Estatal ONMAS Tamaulipas 2013; UAMCEH-UAT, Cd. Victoria, 19 de abril (Cada problema 7 puntos, no se permiten calculadoras ni celulares. Duración: 4 hrs
1N. Encontrar todos los enteros positivos n tales que 3n+4 es múltiplo de 5.
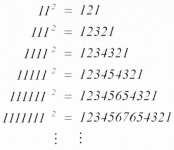
Razonamiento diagramático --en problemas de factorización
En este post voy a comentar sobre el método de reagrupamiento para factorizar una ecuación cuadrática y su correspondiente solución diagramática. Ilustro con un caso particular de toda
Una familia de problemas cuadráticos
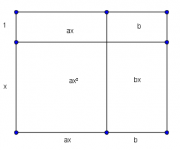
En una ecuación cuadrática, si se puede factorizar entonces se puede representar como rectángulo --con uno de sus factores la base y el otro la altura.
Consideremos el problema de factorizar la ecuación cuadrática
ax2+(a+b)x+b=0
(donde a,b son enteros positivos).
Un problema geométrico --propuesto por Orlando Ochoa
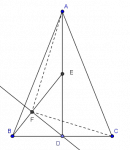
En el entrenamiento de la semana pasada (19, 20 y 21 de octubre) le tocó a Orlando Ochoa Castillo decidir la selección Tamaulipas de la XXVI OMM --con su entrenamiento y su examen selectivo del domingo en la mañana.
El viernes 19 me tocó recibir a Orlando (a las 4 PM) y presentarlo a los preseleccionados. Orlando inició su entrenamiento con el problema que abajo se dicute. Yo decidí quedarme un rato en el aula en que tuvo lugar la sesión de Orlando y, sin más que hacer, me puse a resolverlo... (pero al final tuve que recurrir a la geometría analítica pues la idea creativa no llegó a mi cabeza...). El problema es el siguiente:
IMO 2012 --los problemas de geometría
En los problemas de la IMO, la dificultad para un aficionado a las matemáticas de concurso (como el que esto escribe) no es el resolverlos (esa es casi una imposibilidad) sino el entender las soluciones publicadas. Voy a comentar en este post las soluciones de los problemas 1 y 5 de la 53 International Mathematical Olympiad (2012) que se celebró en Mar del Plata (Argentina) del 4 al 16 de julio.
Para el problema 1 me faltaba un teorema, para el 5 el plan de solución. Es decir, para el 5 la solución publicada la podía seguir, pero me quedaba la incógnita de por qué o cómo esa ruta de solución era la correcta o por qué.

Discusión sobre un problema de geometría
En este post voy a tratar de ilustrar, a través de un problema de geometría, la tesis de que la competencia experta en el problem solving requiere de una combinación de técnicas y conocimiento conceptual (de competencias conceptuales pero también procedimentales).
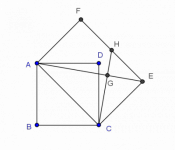
Un problema no trivial de geometría
Tomando como base la diagonal AC de un cuadrado ABCD, se construye un rectángulo ACEF de altura el lado del cuadrado y con D dentro de él.
Si H es el punto medio de EF y G es la intersección de AE con CH, demostrar que