Un problema geométrico --propuesto por Orlando Ochoa

En el entrenamiento de la semana pasada (19, 20 y 21 de octubre) le tocó a Orlando Ochoa Castillo decidir la selección Tamaulipas de la XXVI OMM --con su entrenamiento y su examen selectivo del domingo en la mañana.

El viernes 19 me tocó recibir a Orlando (a las 4 PM) y presentarlo a los preseleccionados. Orlando inició su entrenamiento con el problema que abajo se dicute. Yo decidí  quedarme un rato en el aula en que tuvo lugar la sesión de Orlando y, sin más que hacer, me puse a resolverlo... (pero al final tuve que recurrir a la geometría analítica pues la idea creativa no llegó a mi cabeza...). El problema es el siguiente:

En el triángulo $ABC$, con $AB=AC$, $D$ es el punto medio de $BC$ y $E$ el de $AD$. Si $F$ es el pie de la perpendicular bajada desde $D$ al segmento $BE$, demostrar que el ángulo $CFA$ es recto.

Solución creativa (y sintética)

La primera pista que apunta a una solución es ver que --por complementariedad-- los ángulos $FDB$ y $FED$ son iguales. De aquí que sean iguales --por suplementariedad--  los ángulos $AEF$ y $CDF$.

De esta igualdad de ángulos --y con una buena figura-- se tiene que llegar a ver que el plan adecuado es demostrar que los ángulos $DFC$ y $EFA$ son iguales o, equivalentemente, que los triángulos $AEF$ y $CDF$ son semejantes.

(Porque, en ese caso, un giro con centro en $F$ y ángulo $DFC$ pone a los triángulos $DFE$ y $CFA$ en posición de Tales o, equivalentemente, se llega a que el cuadrilátero $AFDC$ es cíclico.)

La verdadera dificultad del problema es demostrar esa semejanza. Y aquí puede uno darle vueltas al enunciado, a los datos y a la figura sin aanunca llegar a la idea clave para ejecutar el plan. Un caso de esos en que el plan es de una simplicidad extrema pero su ejecución es desesperantemente elusiva. (La idea clave para demostrar la semejanza es el tercer criterio de semejanza --como se le llama al criterio LAL.)

Razonando de manera dinámica, no es muy difícil ver que --suponiendo la conclusión-- un giro de 90 sobre el punto $E$ lleva al triángulo rectángulo $CDF$ a una posición de Tales con el $CFA$ --quedando el lado $D'C'$ paralelo al $AE$ (Ver figura.) Y se hace evidente que lo que se tiene que demostrar es la proporción $EF/D'F=AE/D'C'$.

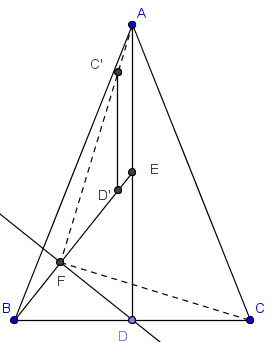
Es decir, $EF/DF=ED/BD$ (en esta última razón es donde se usan los datos de puntos medios). Pero esta proporción es ya evidente --dada la semejanza de los triángulos $EFD$ y $EDB$. El resultado se sigue.

Comentario 

El criterio $LAL$ de semejanza es poco usado --yo diría que ocurre con probabilidad de 1 en 10, si se me permite aventurar una estimación subjetiva.

Es por eso que los problemas diseñados para usar este criterio son difíciles --porque toman por sorpresa al cognizador aun cuando éste conozca ese criterio. Ver mi post http://www.matetam.com/blog/entradas-jmd/reciproco-tales-y-criterio-lal-semejanza

Y ello porque, ya sabiendo que dos ángulos correspondientes son iguales, uno lo que busca es demostrar --de forma "natural"-- la igualdad de otros dos correspondientes. Y esa forma "natural" de demostrar semejanza se convierte en un obstáculo al razonamiento. (Por lo menos eso es lo que a mí me pasó al tratar de resolver este problema.)

Solución analítica

El problema --y su figura correspondiente-- facilita una solución analítica debido a la simetría. Se puede tomar $AD$ como el eje $x$ y $DC$ como el eje $y$ y, sin pérdida de generalidad, las coordenadas de los puntos se pueden fijar de la siguiente manera:
$$A=(0,2); E=(0,1); C=(a,0); B=(-a,0)$$

El plan obvio es entonces calcular las coordenadas de $F$ y después las pendientes de $AF$ y $FC$ y ver que son recíprocas y de signo contrario --con lo cual la demostración es finita.

Para llevar a cabo ese plan, primero calculamos la ecuación de la recta $BE$ --con la fórmula de los dos puntos. Una vez hecho eso se calcula la ecuación de $FD$ con la de punto y pendiente (siendo ésta la recíproca y de signo contrario que la de $BE$.

Ecuación de $BE$: $\frac{y}{x+a}=\frac{1}{a}$. Es decir, $y=\frac{1}{a}x+1$

Ecuación de $FD$: $y=-ax$

Coordenadas de $F$:  $-ax=\frac{x}{a}+1$. Es decir, $x=\frac{-a}{1+a^2}, y=\frac{a^2}{1+a^2}$. Por tanto, $$F=(\frac{-a}{1+a^2},\frac{a^2}{1+a^2})$$
Pendiente de $AF$: $$\frac{\frac{a^2}{1+a^2}-2}{\frac{-a}{1+a^2}}$$
Es decir, $m_{AF}=\frac{2+a^2}{a}$

Pendiente de $CF$: $$\frac{\frac{a^2}{1+a^2}}{\frac{-a}{1+a^2-a}}=\frac{-a}{2+a^2}$$

Comparando las dos pendientes el resultado se sigue.

Los saluda
jmd