Pensamiento lateral (¡¿Alguien me puede explicar eso?!)

Me he encontrado en estos días con el tema del pensamiento lateral y, sobre todo, con  sus acertijos. Y creo que puede ser de alguna utilidad para los lectores de MaTeTaM una discusión sobre esos acertijos y su relación con los chistes y los problemas de matemáticas de concurso. La clave que los une es la interpretación de unos datos desde un cierto punto de vista.

Pensamiento lateral

Como se sabe, el pensamiento lateral es una forma de razonar que se aparta del razonamiento usual (al cual se le llama vertical) y que genera soluciones creativas (en la forma de jugadas inesperadas y, por ello, sorprendentes) a problemas aparentemente insolubles. (Para mayores detalles ver artículo de la Wikipedia.)

El tema se ha puesto de moda en la forma de cursos de creatividad ejecutiva y otros como los juegos gana gana (o ganar ganar), el "último grito" en el discurso de los administradores. 

La clave de su éxito --creo-- es que revela o descubre algo de la naturaleza humana que está oculto para la mayoría de los mortales: interpretamos las situaciones prácticas en un contexto (o framing o marco de interpretación) que podríamos llamar preferente, es decir, el marco usual.

Piense el lector en un globo y en la acción de picarlo con un alfiler. Ahora trate de explicar la siguiente situación: Con un alfiler se pica un globo sin que éste haga ruido ni se le salga el aire.

Lo que tenemos que preguntarnos aquí es ¿bajo qué condiciones un globo no se desinfla ni hace ruido al picarlo con un alfiler?

Debería ser claro de este ejemplo que el framing preferente (globo inflado) falla y no queda más que cambiarlo atendiendo al contexto específico en que se aplique. (No es obligatorio ¡que el globo esté inflado!)

Efecto sorpresa del cambio de marco interpretativo

Muchos de los acertijos de pensamiento lateral explotan ese rasgo de la cognición humana que he llamado el framing preferente o marco usual, y cuando llega la solución (sea que uno la encuentre o nos la digan) el resultado es la sorpresa.

("¿Por qué no se me había ocurrido antes?") En esto, los acertijos del pensamiento lateral se parecen a los buenos chistes --en los cuales el cambio de framing conduce a la risa. Considere el siguiente ejemplo (en donde "verduras orgánicas" tiene dos interpretaciones):

La mujer llama por teléfono a la oficina de su marido y le pide a éste que de regreso a casa compre verduras orgánicas para la cena.

Cumpliendo con la petición de su esposa, al salir del trabajo el marido va al supermercado y empieza a buscar verduras orgánicas. Pero como no sabe identificarlas mejor pregunta a un empleado sobre su ubicación.

Pero el empleado recién reclutado no sabe de qué le está hablando el apurado marido. Así que éste, ya un tanto desesperado, le explica: esas verduras son para mi esposa y... no sé cómo explicarte... mira, lo importante es saber si se han rociado con químicos venenosos.

El empleado ahora sí parece entender y le responde: No señor, eso tiene usted que hacerlo por su cuenta.

Notemos que el empleado interpreta la frase "si se han rociado con químicos venenosos" en un marco de interpretación influido quizá por las series policiacas. Si bien mucha de la culpa es del marido en apuros al no explicar correctamente lo que deseaba.

Prejuicios y presuposiciones

Todos los humanos tenemos prejuicios o presuposiciones que se manifiestan en reglas de inferencia. Y ello nos permite juzgar rápido y sin vacilaciones las situaciones usuales.

Pero hay situaciones no convencionales o poco usuales en las cuales ese framing preferente fracasa --en aportar una explicación adecuada. Consideremos el siguiente ejemplo ya clásico de acertijo de pensamiento lateral:

Un hombre entra a la cantina y pide, con urgencia, un vaso de agua al cantinero. Éste saca su pistola y le apunta con ella amenazando con disparar. El hombre le da las gracias al cantinero y se va. ¿Tiene esto algún sentido?

Sí. El hombre tenía un ataque de hipo.

O este otro:

Una mujer tenía dos hijos que le nacieron el mismo año, el mismo día y a la misma hora, pero no son gemelos. ¿Alguien me puede explicar eso?

Sí. La mujer tuvo triates pero uno no sobrevivió.

¿Qué tenemos aquí? Lo que tenemos son situaciones aparentemente inexplicables y se pide encontrar un posible contexto que explique los datos. Uno debe preguntarse ¿bajo que condiciones esta situación tiene una lógica? (o, ¿qué contexto explica los datos de la situación?)

Out of the box (las presuposiciones como obstáculo)

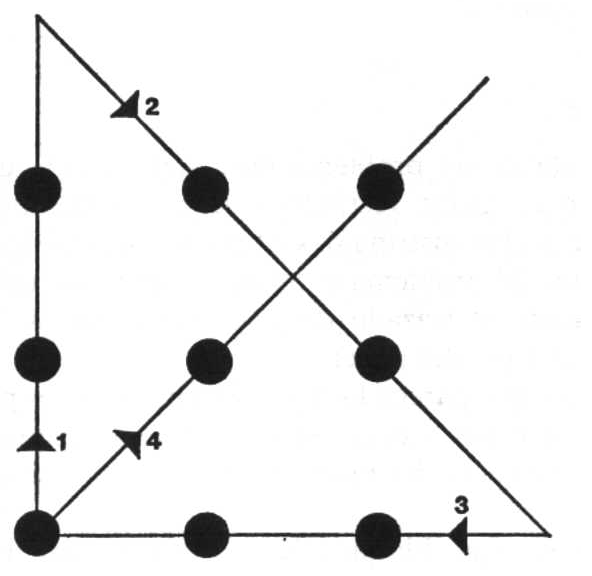
El pensamiento lateral está asociado al de "pensar fuera de la caja" (out the box), el cual está representado por el acertijo prototipo denominado acertijo de los nueve puntos (o firma del diablo): nueve puntos formando un cuadrado (la caja) deben ser cubiertos todos con cuatro líneas rectas sin levantar el lápiz. 

Después de que se ha buscado sin éxito una solución y alguien la muestra, la moraleja obvia es que nuestras presuposiciones son restricciones autoimpuestas, y que  ellas impiden llegar a una solución: nada en el enunciado restringe a no salirse de los límites del cuadrado (la caja).

El huevo de Colón y el problem solving

Una idea brillante puede parecer simple o fácil después de que se conoce. A esta posibilidad se refiere el relato del huevo de Colón:

Los críticos de Cristobal Colón minimizaban su hazaña del descubrimiento de América asegurando que cualquiera lo pudo haber hecho, que no fue la gran cosa. Cristóbal Colón en respuesta los retó a que pararan un huevo sobre una de sus puntas. Después de haber fracasado en su intento los críticos le pidieron a Colón que lo parara él mismo. Colón entonces cogió el huevo, golpeó su punta suavemente sobre la mesa (de manera que al quebrarse levemente quedara plana) y lo colocó de pie (en equilibrio) sobre ella.

La historia lleva un mensaje acerca de la vida y el aprendizaje: cuando ya sabes cómo hacerlo, la solución resulta obvia para tí; lo verdaderamente difícil es ser el primero en hacerlo. O, como dice la Real Academia Española,

el Huevo de Colón es "...una cosa que aparenta tener mucha dificultad pero resulta ser fácil al conocer su artificio."

El siguiente acertijo de geometría refleja la definición de la Real Academia:

Las diagonales de dos caras de un cubo convergen en un vértice. ¿Cuánto mide  el ángulo que forman?

Mide 60 grados, pues forman un equilátero al unir los otros extremos de las diagonales.   

(Otra moraleja o enseñanza del relato del huevo de Colón es que, incluso si tú mismo descubriste algo nuevo, al momento de comunicarlo lo tienes que simplificar; y esa simplificación no refleja las dificultades (el esfuerzo, las frustraciones, etc.) que tuviste para encontrarlo. Y no faltará alguien que diga que el resultado era obvio.)

Consideremos, para finalizar, el principio de las pichoneras (o de las casillas) usado en problemas de combinatoria (y de concurso):

Si n pichones deben dormir en n-1 nidos, entonces dos de ellos duermen juntos.

Evidente ¿no es cierto? Sí, pero sólo después de que se ha usado en la resolución de problemas concretos de combinatoria. (También se le llama Principio de las casillas de Dirichlet, por haber sido este matemático quien lo usó por primera vez en el siglo XIX.)

Enseguida dos instancias de uso:

En cualquier conjunto de siete enteros siempre hay dos cuya suma o diferencia es múltiplo de 11.

Para una solución ver el problema siete enteros en MaTeTaM

En cualquier conjunto de cinco enteros siempre hay tres cuya suma es múltiplo de 3.

(Solución: de deja como ejercicio para el lector.)

Los saluda
jmd