En este post voy a comentar la solución del problema 4 de la IMO 2010 (posiblemente el único de los 6 de este concurso que solamente requiere conocimientos elementales).
Didáctica geométrica --adaptada de la de Hoch y Dreyfus
Elijo como telón de fondo para estos comentarios --un poco como en un eco-- el post denominado Sentido de la estructura algebraica, en el cual comenté que el resolutor de problemas (en ese caso, el estudiante de bachillerato) puede aprender a ver las claves de la solución del problema en el enunciado, trayendo a presencia (haciendo conexiones con) conceptos y procedimientos anteriormente aprendidos.
Bueno, quiero decir, ese proceso del tránsito de novicio a experto se puede acelerar a través de una didáctica que tiene un aire de familia con la didáctica ajedrecística (y la de apreciación del arte). Y a esta habilidad experta se llega mediante un entrenamiento anterior en la lectura de las claves. Es decir, mediante un entrenamiento en decodificación (en términos de conocimientos relevantes) de los datos del problema.
Supongamos que el cognizador ya ha estudiado los teoremas básicos de la geometría del círculo y ha resuelto problemas que son instancias de uso de esos conocimientos. Puede ser, sin embargo, que le falte adquirir el sentido de la estructura de una configuración geométrica.
Haciendo eco de las definiciones de Hoch y Dreyfus mencionadas en el post arriba mencionado, se puede decir que el cognizador tiene sentido de la estructura geométrica si:
- puede reconocer una estructura familiar en su forma más simple (por ejemplo, el teorema de las cuerdas cruzadas);
- ha adquirido la competencia de reconocer una estructura familiar dentro de una configuración compleja;
- es capaz de elaborar un plan de solución para explotar una estructura familiar
Ilustrado con el teorema de las cuerdas cruzadas, el primer nivel sería que a partir de la configuración
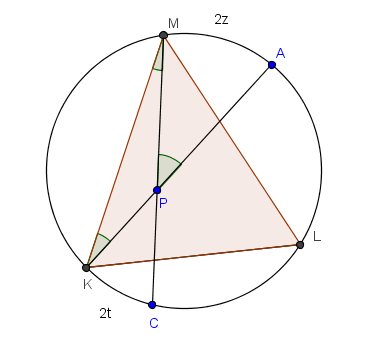
el cognizador pudiera traer a presencia el teorema de las cuerdas cruzadas (y el significado de ángulo inscrito) para concluir que el ángulo formado por las cuerdas es t+z (y que los ángulos en M y K del triángulo MKP son, respectivamente, t y z).
El segundo nivel sería la capacidad de ver eso mismo pero en la configuración compleja siguiente
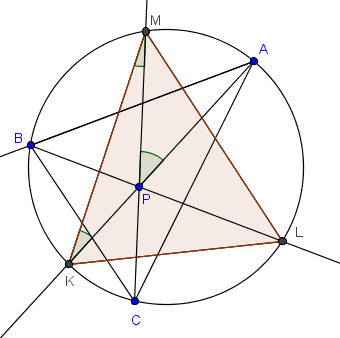
El tercer nivel sería: ser capaz de sospechar (elaborar la conjetura de) que, en la solución de un problema, el teorema de las cuerdas cruzadas puede ser útil, y elaborar en consecuencia un plan de solución que lo incluya. (Ver más abajo el análisis previo del problema comentado en este post.)
Como forma de entrenamiento, se le pueden presentar al aprendiz diversas formas en que las dos configuraciones anteriores pueden ocurrir. Primero con datos concretos, y pedirle que 1) verbalice la estructura, 2) que genere una configuración similar en que la estructura esté presente, y finalmente 3) que la resuelva (es decir, que calcule el valor del ángulo formado por las cuerdas, dadas las medidas de los arcos interceptados).
Primero se le presentarían configuraciones del primer nivel hasta que llegue a ver sin problemas la estructura; después se le presentarían configuraciones del segundo nivel hasta que domine la visualización del teorema; finalmente debería resolver problemas en que el teorema sea la herramienta principal.
Disclaimer
Me apresuro a decir que el método de las entrevistas didácticas recomendado por Hoch y Dreyfus no se adapta a la ecología escolar. Por varias razones. La primera es que el profesor (suponiendo que conozca el método y sepa geometría) no estaría dispuesto a elaborar tanto material de enseñanza por el mismo precio.
La segunda es que posiblemente el profesor no encontraría alumnos dispuestos a realizar las actividades e interrogatorios que implican las entrevistas didácticas. (Y eso en el caso inverosímil de que encontrara alumnos que ya tuviera nociones de geometría...)
Ni bueno ni malo, es solamente un ejemplo de que la mejor solución didáctica es con demasiada frecuencia imposible de realizar --y bueno, este hecho debería ser también una lección para los reformadores educativos... (La didáctica realmente existente sigue siendo la del gis y el pizarrón... es la más económica para el profesor y también, posiblemente, para los alumnos.)
La moraleja de estas aseveraciones --en caso de que no sean un reflejo del pesimismo educativo del que esto escribe-- es que el adolescente que realmente desee ser competente en matemáticas de concurso debe aprender a ser autodidácta.
El problema 4 de la IMO 2010
Sea P un punto en el interior del triángulo ABC con circunferencia circunscrita Γ. Las rectas AP,BP,CP cortan otra vez a Γ en los puntos K,L,M, respectivamente. La recta tangente a Γ en C corta a la recta AB en S. Demostrar que si SC=SP entonces MK=ML.
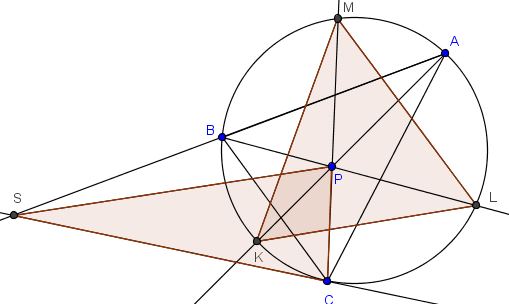
Comentarios generales sobre el problema
El problema es difícil (por algo es el 4 de la IMO). Pero no por los conocimientos de geometría que su solución requiere, sino porque, a pesar de que solamente requiere geometría básica del círculo, las claves de su solución están escondidas en el enunciado y en la configuración geométrica a que éste da lugar.
Los conocimientos requeridos son:
- Potencia de un punto exterior con tangente y secante
- Teorema converso del anterior (si bien, generalmente, el converso nunca se demuestra en un curso básico): si PB2=PC⋅PA entonces PB es tangente en B al circuncírculo de ABC
- Concepto de ángulo inscrito y semi-inscrito, su relación con el central y el arco interceptado por sus lados, así como su uso operativo en problemas. (El lector podría navegar los GBC-teoremas de MaTeTaM partiendo del teorema del ángulo central.)
- Teorema de las cuerdas cruzadas y su uso operativo en problemas.
- Teorema del triángulo isósceles. Y otros...
Análisis previo y construcción del plan
Los datos realmente usables en el enunciado del problema 4 de la IMO 2010 son:
- 1) La tangente al circuncírculo de ABC (de donde se puede calcular la potencia de S)
- 2) El hecho de que SP=SC
- 3) Y, bueno, de la figura se pueden ver varios pares de ángulos inscritos iguales por tener el mismo arco interceptado...
Esto último sugiere construir un plan de cacería de ángulos donde se intentaría llegar a que los ángulos en la base KL del triángulo KLM son iguales, usando los datos anteriores. (Un plan alternativo podría ser el uso de triángulos semejantes --parece que hay varios pares semejantes) y ligar las razones obtenidas para llegar a MK/ML=1 o a algo parecido.)
La pregunta clave es: ¿cómo usar los datos 1) y 2) para una cacería eficaz de ángulos?
Descubrimiento de la información (escondida en la configuración)
Primer descubrimiento
Si el cognizador hace un análisis previo como el anterior (o uno mejor), entonces debería llegar a que AP es tangente en P al circuncírculo de APB (converso de la potencia de un punto). Pues SC2=SB⋅SA, por dato y potencia de un punto. Pero, CPS es isósceles. De ahí que SP2=SB⋅SA.
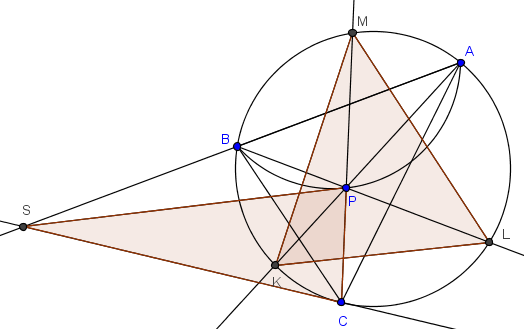
Con esto ya se tienen dos círculos para emprender la cacería de ángulos. Este descubrimiento debería fortalecer la creencia de que el problema es resoluble mediante cacería de ángulos.
Segundo descubrimiento
La pregunta clave en este punto es ¿cómo ejecutar el plan de llegar a ángulos iguales en la base KL del triángulo KLM? Es decir, de manera más concreta, ¿cómo paso de ángulos iguales en la base CP del triángulo CPS a ángulos iguales en la base KL del KLM?
La respuesta podría ser el teorema de las cuerdas cruzadas. (Esta conclusión podría llegar después de que la cacería llega a un punto muerto y la pregunta anterior es obligada.)
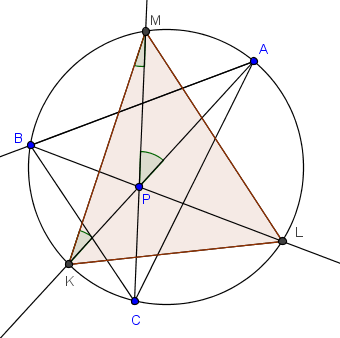
¿Por qué es importante aquí este teorema de las cuerdas cruzadas? Bueno, porque en P se cruzan muchas cuerdas (3, de hecho), y el teorema permitiría pasar de un lado a otro del círculo.
Cacería de ángulos
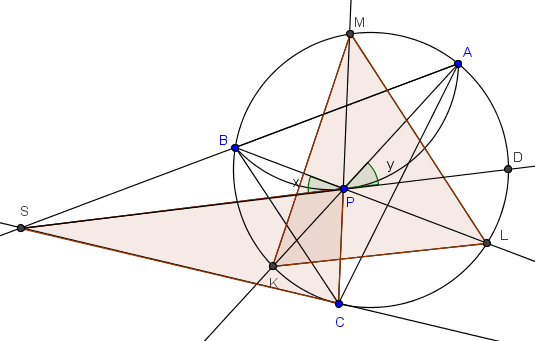
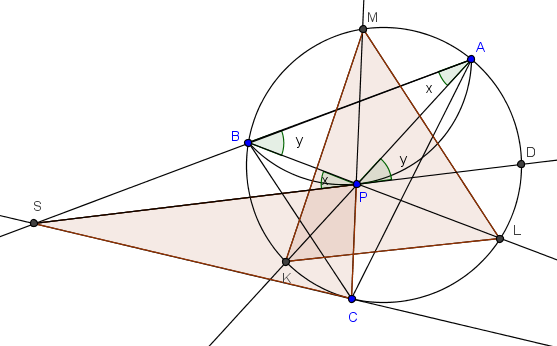
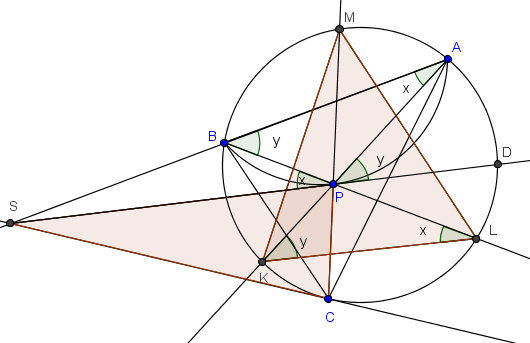
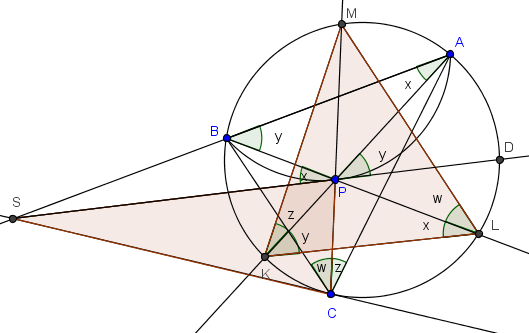
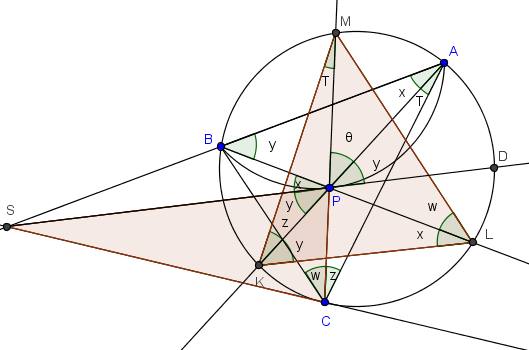
Solución
Una vez dicho esto (y descubierto esto y haber realizado la cacería de ángulos ), la solución se puede escribir en dos renglones.
Queremos demostrar y+z=x+w. Si focalizamos las dos cuerdas cruzadas que forman el ángulo θ, entonces podemos aplicar el teorema: θ=T+z. (Semisuma de arcos KC y AM.)
Pero θ+y es ángulo en la base CP del isósceles CPS. Por tanto, mide x+T+w (Nótese que el arco BC mide el doble que x+T.)
Tenemos finalmente la ecuación θ+y=T+z+y=x+T+w. Cancelando T en ella se obtiene z+y=x+w, como se quería.
Los saluda
jmd
PD: El lector podría desear practicar con el siguiente problema más simple (inspirado en el 4 de la IMO 2010).
Sea P un punto en el interior del triángulo ABC con circunferencia circunscrita Γ. Las rectas AP,BP,CP cortan otra vez a Γ en los puntos K,L,M, respectivamente. La recta tangente a Γ en C corta a la recta AB en S. Demostrar que si SP es tangente en P a la circunferencia circunscrita del triángulo ABP, entonces SP=SC.
