Este post introduce los conceptos más básicos de la geometría analítica: distancia entre dos puntos, pendiente de una recta y coordenadas del punto medio. Supone que el lector ya conoce las reglas de representación de puntos en el plano cartesiano de coordenadas.
Parecería fácil elaborar una presentación elemental de la geometría analítica (para bachillerato) por un profesor que la ha estudiado al menos en algún curso universitario. Y lo es, pero hay que pensarle un rato (digamos unos dos o tres días...).
En estos días en que nos llegó el frío y la llovizna, iba a poner un problema de geometría a resolver con geometría analítica. Pero luego me dije: pero en MaTeTaM no se ha abordado el tema de geometría analítica.... Entonces me puse a elaborar un post introductorio que incluyera los conceptos básicos. De acuerdo a los estándares de MaTeTaM debería estar orientado conceptualmente. La primera pregunta que me hice fue ¿cuáles son los conceptos básicos? Y llegué a la conclusión de que
Los conceptos más básicos de la geometría analítica
- Distancia entre dos puntos
- Pendiente de una recta
- Coordenadas del punto medio
Creo que aprendiendo estos conceptos y sus modos de uso ya se puede entrar al problem solving en geometría de coordenadas, y seguir aprendiendo sobre la marcha otros más, con los cuales se podrán resolver problemas cada vez más difíciles.
La fórmula de distancia entre dos puntos se deriva directamente del Teorema de Pitágoras. La pendiente de una recta es una definición de una de sus características (está asociada con la tangente del ángulo que forma la recta con el eje x). La fórmula del punto medio se puede ver ya como un teorema cuya demostración (una de ellas) se basa en los conceptos de pendiente y distancia entre dos puntos. (La ecuación de una recta --no abordada en este post-- se puede ver como la descripción algebraica de la recta en un sistema cartesiano de coordenadas.
Los conocimientos previos requeridos para aprender estos tres conceptos son: Teorema de Pitágoras (para distancia), Teorema de Tales (para pendiente), Congruencia de triángulos (para punto medio), y pues también la representación de puntos vía coordenadas en un sistema cartesiano de ejes rectangulares (el sistema usual).
Distancia entre dos puntos
La siguiente figura debería ser suficiente para que el lector se apropie de la idea de la demostración de la fórmula de distancia entre dos puntos:
d2(A,B)=(x−X)2+(y−Y)2

Comentemos, de paso, que en la lectura de la figura es obligatorio saber el concepto de coordenadas de un punto. Por ejemplo, C tiene coordenadas (x,Y) porque está sobre la vertical que pasa por B (con abscisa x) y por la horizontal que pasa por A (con ordenada Y).
Aclaro también que, en la figura, √(y−Y)2 se refiere al valor absoluto de la diferencia (|y−Y|), es decir, a la distancia entre las dos alturas y y Y. De hecho, la apelación al valor absoluto no es necesaria aquí como se ve en el lema que se presenta abajo... pero ya había hecho la figura...
Pendiente de una recta

Aparte de su interpretación usual como razón de cambio de la altura respecto al desplazamiento horizontal, la pendiente se
puede ver también como la tangente (en el sentido trigonométrico) del ángulo que forma la recta con el eje x. En la figura, tal ángulo es el \angCAB. Notemos que la pendiente puede ser negativa, en cuyo caso la recta baja de izquierda a derecha. Si atendemos a los ejes en la figura, x=2 y X=−3, se manera que x−X=2−(−3)=5. En el cálculo de m se están considerando los signos de las coordenadas de los puntos.
Notemos también que si la recta es vertical la fórmula da una indeterminación pues se tendría una división entre cero. En ese caso se dice que la pendiente es infinita. Si, por otro lado, la recta es horizontal, su pendiente es cero.
Coordenadas del punto medio de un segmento
Lema: El promedio de dos números está exactamente a la mitad del camino entre ellos
Demostración: Sean a,b los números. Sin pérdida de generalidad se puede suponer a<b. Entonces, la distancia entre ellos es b−a (y la mitad de esta distancia es b−a2. Entonces, el punto medio entre a y b es:
a+b−a2=2a+b−a2=a+b2
Nota: El lector haría bien en checar todos los casos de signos de a y b. Por ejemplo, si ambos son negativos, digamos -9 y -3, entonces la distancia entre ellos se obtiene restando el mayor (-3) menos el menor (-9).
Teorema: Las coordenadas del punto medio de un segmento son las coordenadas promedio de los extremos del segmento.
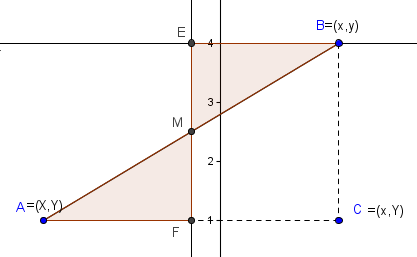
Demostración: Con referencia a la figura, donde M es el punto medio de AB, tracemos una vertical por M y las horizontales por B y A, respectivamente. Se forman los triángulos rectángulos AFM y BEM, los cuales son congruentes: por definición de punto medio, AM=MB y se puede aplicar el criterio ALA. De aquí que EM=MF y AF=EB=FC. Es decir, M es punto medio de EF y F es punto medio de AC. Aplicando el lema se obtiene el resultado.
Epílogo
Creo que la forma usual en que se introducen en los libros de texto estos conceptos no le da una oportunidad al problem solving (como recomienda el enfoque actual). La consigna tradicional usual ("estas son las fórmulas y resuelvan estos 20 ejercicios") discrimina (en el sentido de que los margina, los deja a un lado o los ignora) a los estudiantes con más aspiraciones respecto a las matemáticas y su educación.
Creo que el profesor (y el texto sobre todo --pues el profesor no tiene tiempo de andar haciendo planeaciones) debería presentar el por qué de las fórmulas antes de entregarlas como algo "natural" o ya sabido o como la pildora que se tienen que tragar. Ello daría oportunidad a los más cabecillas (digamos al 20% de la clase) de interesarse en las deducciones y demostraciones.
Creo también que se puede diseñar una secuencia didáctica donde las consignas sean resolver los subproblemas que surgen de las anteriores deducciones y demostraciones. Aunque quizá eso sea mucho pedir... por el mismo precio...
Los saluda
jmd
PD: Faltan los ejercicios y los problemas que reforzarían el aprendizaje de estos tres conceptos básicos. Los pondré en la sección de problemas. La ecuación de una recta la discutiré en otro post pues, a pesar de que es el cuarto concepto básico, su discusión requiere más espacio dado que los matices y casos son muchos. Por ejemplo, sobre la ecuación de una recta hay dos tipos de problemas:
--Dada la ecuación, extraer la información que contiene (por ejemplo, su pendiente, sus intercepciones con los ejes).
--Dados un punto de la recta y su pendiente (así sea de manera implícita), determinar la ecuación de la recta.
