Julio 2012
Discusión sobre un problema de geometría
En este post voy a tratar de ilustrar, a través de un problema de geometría, la tesis de que la competencia experta en el problem solving requiere de una combinación de técnicas y conocimiento conceptual (de competencias conceptuales pero también procedimentales).
Un problema no trivial de geometría
Tomando como base la diagonal AC de un cuadrado ABCD, se construye un rectángulo ACEF de altura el lado del cuadrado y con D dentro de él.
Si H es el punto medio de EF y G es la intersección de AE con CH, demostrar que
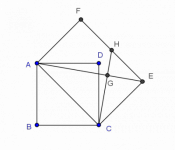
IMO 2012 --los problemas de geometría
En los problemas de la IMO, la dificultad para un aficionado a las matemáticas de concurso (como el que esto escribe) no es el resolverlos (esa es casi una imposibilidad) sino el entender las soluciones publicadas. Voy a comentar en este post las soluciones de los problemas 1 y 5 de la 53 International Mathematical Olympiad (2012) que se celebró en Mar del Plata (Argentina) del 4 al 16 de julio.
Para el problema 1 me faltaba un teorema, para el 5 el plan de solución. Es decir, para el 5 la solución publicada la podía seguir, pero me quedaba la incógnita de por qué o cómo esa ruta de solución era la correcta o por qué.

