Combinatoria

Sea $n > 1$ un entero positivo y sean $d_1 < d_2 < ... < d_m$ sus $m$ enteros positivos de manera que $d_1 = 1$ y $d_m = n$. Lalo escribe los siguientes $2m$ números en un pizarrón:

$d_1 , d_2 , ... , d_m , d_1 + d_2 , d_2 + d_3 , ... , d_{m-1} + d_m , N$

donde $N$ es un entero positivo. Después Lalo borra los números repetidos (por ejemplo, si un número repetido aparece 2 veces, el borrará uno de los dos). Después de esto, Lalo nota que los números en el pizarrón son precisamente la lista completa de divisores positivos de $N$. Encuentra todos los posibles valores del entero positivo $n$.

Sea $n$ un entero positivo. En un jardín de $n \times n$ cuyos lados dan al Norte, Sur, Este y Oeste se va a construir una fuente usando plataformas de $1 \times 1$ que cubra todo el jardín.

Ana colocará las plataformas todas a diferente altura. Después, Beto pondrá salidas de agua en algunas de las plataformas.

El agua de cada plataforma puede bajar a las plataformas contiguas (hacia el Norte, Sur, Este y Oeste) que tengan menor altura que la plataforma de donde viene el agua, siguiendo su flujo siempre que pueda dirigirse a plataformas de menor altura. El objetivo de Beto es que el agua llegue a todas las plataformas.

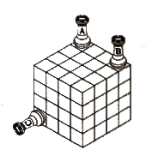
Sea $n$ un entero positivo. David tiene 6 tableros de ajedrez de $n \times n$ que ha dispuesto de manera que formen las 6 caras de un cubo de $n \times n \times n$. Se dice que dos casillas $a$ y $b$ de este nuevo tablero cúbico están alineadas si podemos conectarlas por medio de un camino de casillas $a = c_1, c_2, \dots, c_m = b$ de manera que cada pareja de casillas consecutivas en el camino comparten un lado, y los lados que la casilla $c_i$ comparte con sus vecinas son lados opuestos del cuadrado $c_i$, para $i = 2, 3, \dots, m-1$. Diremos que dos torres colocadas sobre el tablero se atacan; si las casillas que ocupan están alineadas. David coloca algunas torres sobre el tablero de forma que ninguna ataque a otra.

Un número $x$ es Tlahuica si existen números primos distintos $p_1, p_2 \dots, p_k$ tales que

Determina el mayor número Tlahuica que satisface las dos propiedades siguientes:

1. 0 < x < 1
2. existe un número entero $0 < m \leq 2022$ tal que $mx$ es un entero.

A una cena llegan 3 matrimonios. Se quieren sentar alrededor de una mesa redonda de manera que nadie quede junto a su pareja. ¿De cuántas formas se pueden acomodar si Ana ya tiene un lugar asignado fijo?

Julieta y Edwin juegan al siguiente juego. Se empieza con una bolsa que contiene 2022 piedras. Se juega por turnos alternados y cada jugador puede hacer lo siguiente:

• Si el número de piedras en la bolsa es par, el jugador puede tomar una piedra o la mitad de las piedras.
• Si el número de la bolsa es impar, tiene que tomar una sola piedra.

Gana quien tome la última piedra. Julieta empieza el juego. 

Determina quién tiene una estrategia ganadora y explícala.

Mauricio se está probando ropa en una tienda. Está indeciso entre 4 camisas, 7 suéteres, 3 sudaderas y 3 pantalones, todos estos artículos distintos. Comprará exactamente 3 artículos, todos de diferentes tipos (es decir, no dos camisas y un suéter o tres pantalones, etc.). ¿De cuántas formas Mauricio podrá hacer sus compras?

Dos personas A y B van a jugar un juego alternando turnos; A toma el primer turno. Para el juego está dibujada sobre un papel una cuadrícula de 7 × 7. En cada turno se borran algunos de los cuadritos como sigue: El jugador en turno escoge un cuadrito y borra toda la columna y el renglón a los que pertenece ese cuadrito dentro de la porción rectangular donde está en ese momento el cuadrito. Por ejemplo, si al principio A escoge
el cuadrito marcado con 1 en la figura (a) de abajo, a B le queda la figura (b) y, si él escoge el cuadrito marcado con 2, entonces para el siguiente turno a A le queda la figura (c).

En una fecha escrita de la forma aa/mm/yy o a/m/yy se multiplican los digitos usados para escribirlas, por ejemplo 24/12/22 da 2x4x1x2x2x2=64 o 5/8/22 da 5x8x2x2=160. ¿Cuántas fechas de la década de los 2020's cumplen que la multiplicación de los dígitos da 120?

Se van a construir piezas rectangulares de área 240 cm² y con ambos lados entero. ¿De cuántas formas distintas se puede hacer?