Publicaciones Recientes
México entra al top 20 en la IMO 2013
Tarde pero sin sueño --como dicen en Viento Libre--, la noticia es que los mexicanos entraron este año 2013 al top 20 (con 3 platas y 3 bronces) en la Olimpiada Internacional de Matemáticas (IMO, por sus siglas en inglés).
La IMO se celebró del 18 al 28 de julio en Santa Marta, Colombia, uno de los mejores lugares turísticos del Caribe colombiano (según la Wikipedia).
Método Singapur --para razonar problemas verbales elementales
Llamo problemas verbales (word problems) a los problemas razonados con los que se introduce (o debería introducirse) el razonamiento matemático en la escuela primaria (en quinto y sexto año por lo menos). Voy a ilustrar el tema con
Un ejemplo
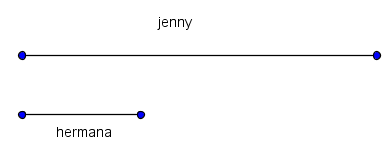
Jenny tiene 7 pesos y su hermana 2. Después de que su madre les da una misma cantidad de pesos Jenny tiene el doble que su hermana. ¿Cuánto recibieron de su madre?
Solución algebraica
Relación desfasada de edades
Beto tiene el doble de la edad que Sandra tenía cuando Beto era de la edad que ahora tiene Sandra. Cuando Sandra tenga la edad que ahora tiene Beto, la suma de sus edades será 45 años. ¿Qué edad tienen?
Velocidad promedio de un viaje
Miguel viajó en su auto de la ciudad P a la ciudad Q. En la primera hora recorrió 1/3 de la distancia entre las ciudades y en la segunda 1/5. Llegó a su destino después de dos horas más durante las cuales viajó a una velocidad de 42 km/h. Calcular la velocidad promedio de todo el viaje. (Nota: la velocidad promedio se define como distancia/tiempo.)
Eficiencia ensayística estudiantil
Abel y Brenda estudian sociología en la universidad. Para elaborar sus ensayos de fin de cursos utilizan el método estándar de copiar (de la Web) y pegar (en su ensayo). Usando Google Drive pueden elaborar juntos (pero cada quien desde su laptop) un ensayo de 48 páginas en 6 horas. Sin embargo, trabajando solo, Abel se tarda 16 horas más que Brenda --para elaborar un ensayo de 48 páginas . ¿Cuánto tarda Brenda para elaborar un ensayo de 48 páginas --usando copy and paste e independientemente de calidad?
Media y mediana
Encontrar todos los números reales x con la propiedad de que la mediana de x,6,4,1,9 coincide con su media.
Calcular una proporción
Un grupo de n alumnos presentó el examen de admisión en una universidad. Si se sabe que pasaron exactamente 2/3 de los varones y exactamente 3/4 de las mujeres, y que el número de mujeres que pasaron es igual al número de varones que pasaron el examen, calcular el porcentaje de alumnos que pasaron el examen.
Valor de una suma dadas ciertas condiciones
Los enteros positivos a,b,c satisfacen el sistema
c2−a2−b2=101
ab=72
Encontrar el valor de a+b+c
Área del triángulo si...
Si los enteros positivos a,b,c son los lados de un triángulo rectángulo, y son tales que a<b<c y a+c=49. Encontrar el área del triángulo.
Cambio de base ¿cuál es la base?
Si el número 86 en base 10 se representa como 321 en base b ¿cuál es la representación en base 10 del número 123 en base b?
