Publicaciones Recientes
OLIMPIADA MATEMATICAS Abril 28, 2017?
Hola
Saben sobre la Guia para apoyar a alumnos de 6 grado de primaria que participaran en la Olimpiada de Matematicas este 28 de Abril?
Saludos
AB
31a Olimpiada Mexicana de Matemáticas en Tamaulipas
Comienza el proceso de la 31a Olimpiada Mexicana de Matemáticas en Tamaulipas. Adjunto a este mensaje encontrarán la convocatoria y el cartel promocional del evento.
Inicio de la 31a Olimpiada Mexicana de Matemáticas en Tamaulipas
Comienza el proceso de la 31a Olimpiada Mexicana de Matemáticas en Tamaulipas. Adjunto a este mensaje encontrarán la convocatoria y el cartel promocional del evento.

Aclaraciones sobre el Examen Invitacional de la OMM
Calendario dodecaédrico con origami 2017
Para hacer el calendario sólo tienen que descargar, imprimir, doblar y armar. Aquí está el video con las intrucciones de armado que hicimos para la versión 2010.
¡Descanse en paz Prof. José Muñoz Delgado!
Hace varios días falleció el Prof. José Muñoz Delgado, fundador de MaTeTaM, en el Hospital de Cardiología 34 del IMSS en la ciudad de Monterrey, NL.
El Prof. Muñoz era un hombre entregado al estudio y al uso de la lógica, siempre buscaba impulsar estos valores en sus estudiantes y sus hijos. Ingeniero de formación, con maestría en comunicación y autodidacta, logró instruirse a sí mismo en matemáticas avanzadas y filosofía.
Tangentes si y sólo si perpendiculares
Sea $ABCD$ un cuadrilátero inscrito en una circunferencia, $l_1$ la recta paralela a $BC$ que pasa por $A$ y $l_2$ la recta paralela a $AD$ que pasa por $B$. La recta $DC$ corta a $l_1$ y $l_2$ en los puntos $E$ y $F$, respectivamente. La recta perpendicular a $l_1$ que pasa por $A$ corta a $BC$ en $P$ y la recta perpendicular a $l_2$ por $B$ corta a $AD$ en $Q$. Sean $\Gamma_1$ y $\Gamma_2$ las circunferencias que pasan por los vértices de los triángulos $ADE$ y $BFC$, respectivamente. Demuestra que $\Gamma_1$ y $\Gamma_2$ son tangentes si y sólo si $DP$ es perpendicular a $CQ$.
Problema clásico con solución atípica
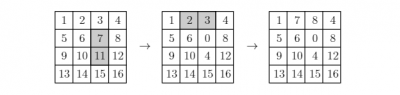
En una cuadrícula de $ n \times n$ se escriben los números del 1 al $n^2$ en orden, por renglones, de manera que en el primer renglón aparecen los números del 1 al n, en el segundo los números del n+1 al 2n, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen esos dos cuadraditos. Por ejemplo, aquí abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de 4x4: primero restando 7 a los cuadraditos sombreados y luego sumando 5 a los sombreados.
Múltiplo de 7 con dígitos consecutivos
Decimos que un número entero no-negativo $n$ contiene a otro número entero no-negativo $m$, si los dígitos de su expansión (o desarrollo) decimal aparecen en forma consecutiva en la expansión (o desarrollo) decimal de $n$. Por ejemplo 2016 contiene a 2,0,1,6, 20, 16, 201 y 2016. Determina el mayor número entero $n$ que no contiene a ningún múltiplo de 7.
Desigualdades con parte entera
Encuentra el menor número real $x$ que cumpla todas las siguientes desigualdades:
$$ \lfloor x \rfloor < \lfloor x^2 \rfloor < \lfloor x^3 \rfloor < \dots < \lfloor x^n \rfloor < \lfloor x^{n+1} \rfloor < \dots $$
Nota: $\lfloor x \rfloor$ es el mayor entero menor o igual a $x$, es decir, es el único número entero que cumple que $ \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1$.
