XXX OMM 2016
Tangentes si y sólo si perpendiculares
Sea ABCD un cuadrilátero inscrito en una circunferencia, l1 la recta paralela a BC que pasa por A y l2 la recta paralela a AD que pasa por B. La recta DC corta a l1 y l2 en los puntos E y F, respectivamente. La recta perpendicular a l1 que pasa por A corta a BC en P y la recta perpendicular a l2 por B corta a AD en Q. Sean Γ1 y Γ2 las circunferencias que pasan por los vértices de los triángulos ADE y BFC, respectivamente. Demuestra que Γ1 y Γ2 son tangentes si y sólo si DP es perpendicular a CQ.
Problema clásico con solución atípica
En una cuadrícula de n×n se escriben los números del 1 al n2 en orden, por renglones, de manera que en el primer renglón aparecen los números del 1 al n, en el segundo los números del n+1 al 2n, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen esos dos cuadraditos. Por ejemplo, aquí abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de 4x4: primero restando 7 a los cuadraditos sombreados y luego sumando 5 a los sombreados.
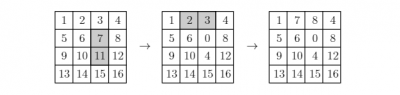
Múltiplo de 7 con dígitos consecutivos
Decimos que un número entero no-negativo n contiene a otro número entero no-negativo m, si los dígitos de su expansión (o desarrollo) decimal aparecen en forma consecutiva en la expansión (o desarrollo) decimal de n. Por ejemplo 2016 contiene a 2,0,1,6, 20, 16, 201 y 2016. Determina el mayor número entero n que no contiene a ningún múltiplo de 7.
Desigualdades con parte entera
Encuentra el menor número real x que cumpla todas las siguientes desigualdades:
⌊x⌋<⌊x2⌋<⌊x3⌋<⋯<⌊xn⌋<⌊xn+1⌋<…
Nota: ⌊x⌋ es el mayor entero menor o igual a x, es decir, es el único número entero que cumple que ⌊x⌋≤x<⌊x⌋+1.
Parejas Guerreras
Una pareja de enteros positivos m,n es guerrera si existen enteros positivos a,b,c,d con m=ab,n=cd y a+b=c+d. Por ejemplo, la pareja 8,9 es guerrera pues 8=4⋅2,9=3⋅3 y 4+2=3+3. Se colorean los enteros positivos de la siguiente manera:
- Empezamos coloreando el 3 y el 5.
- Después , si algún entero positivo no está coloreado y este tiene una pareja guerrera que ya está coloreado, entonces lo coloreamos.
Encuentra todos los enteros positivos que eventualmente se colorean.
Circunferencias con relación de radios
Sean C1 y C2 dos circunferencias tangentes externamente en S tales que el radio de C2 es el triple del radio de C1. Sea l una recta que es tangente a C1 en P y tangente a C2 en Q, con P y Q distintos de S. Sea T el punto en C2 tal que TQ es diámetro de C2 y sea R la intersección de la bisectriz de ∠SQT con el segmento ST. Demuestra que QR=RT
