XXIX OMM 2015

Problema

Problema 6. 29a Olimpiada Mexicana de Matemáticas

Enviado por vmp el 25 de Noviembre de 2015 - 12:57.

Sea $n$ un entero positivo y sean $d_1,d_2, \ldots , d_k$ todos sus divisores positivos ordenados de menor a mayor. Considera el número $$f(n)=(-1)^{d_1}d_1+(-1)^{d_2}d_2+\ldots+(-1)^{d_k}d_k.$$

Por ejemplo, los divisores positivos de 10 son $1,2,5$ y $10$, así que $$f(10)=(-1)^{1}\cdot 1+(-1)^{2}\cdot 2+ (-1)^{5}\cdot 5 +(-1)^{10}\cdot 10=6.$$

Supón que $f(n)$ es una potencia de $2$. Muestra que si $m$ es un entero mayor que $1$, entonces $m^2$ no divide a $n$.

Problema

Problema 5. 29a Olimpiada Mexicana de Matemáticas

Enviado por vmp el 25 de Noviembre de 2015 - 12:52.

Sea $I$ el incentro de un triángulo acutángulo $ABC$. La recta $AI$ corta por segunda vez al circuncírculo del triángulo $BIC$ en $E$. Sean $D$ el pie de la altura desde $A$ sobre $BC$ y $J$ la reflexión de $I$ con respecto a $BC$. Muestra que los puntos $D$, $J$ y $E$ son colineales.

Problema

Problema 4. 29a Olimpiada Mexicana de Matemáticas

Enviado por vmp el 25 de Noviembre de 2015 - 12:47.

Sea $n$ un entero positivo. María escribe en un pizarrón las $n^3$ ternas que se pueden formar tomando tres enteros, no necesariamente distintos, entre $1$ y $n$, incluyéndolos. Después, para cada una de las ternas, María detetermina el mayor (o los mayores, en caso de que haya más de uno) y borra los demás. Por ejemplo, en la terna $(1,3,4)$ borrará los números $1$ y $3$, mientras que en la terna $(1,2,2)$ borrará sólo el número $1$.

Muestra que, al terminar este proceso, la cantidad de números que quedan escritos en el pizarrón no puede ser igual al cuadrado de un número entero.

Problema

Problema 3. 29a Olimpiada Mexicana de Matemáticas

Enviado por vmp el 24 de Noviembre de 2015 - 11:23.

Sea $\mathbb{N}=\{1, 2, 3, \ldots \}$ el conjunto de los números enteros positivos. Sea $f:\mathbb{N} \rightarrow \mathbb{N}$ una función, la cual asigna a cada número entero positivo, un número entero positivo. Supón que $f$ satisface las siguientes condiciones:

$f(1)=1$
Para todos $a,b$ enteros positivos, se cumple que
$$f(a+b+ab)=a+b+f(ab)$$

Encuenta el valor de $f(2015)$

Problema

Problema 2. 29a Olimpiada Mexicana de Matemáticas

Enviado por vmp el 24 de Noviembre de 2015 - 11:15.

Sean $n$ un entero positivo y $k$ un entero entre $1$ y $n$. Se tiene un tablero de $n \times n$ color blanco. Se hace el siguiente proceso. Se dibujan $k$ rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos $k$ rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de $k$ rectángulos?

Problema

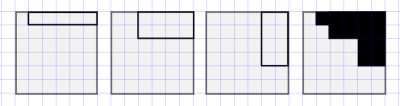
Problema 1. 29a Olimpiada Mexicana de Matemáticas

Enviado por vmp el 24 de Noviembre de 2015 - 11:08.

Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB=\angle CHQ$. Finalmente en el ciruncírculo del triángulo $ABC$ considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP=MQ$.