En este post voy a argumentar que el punto medio de un segmento y la bisectriz de un ángulo son conceptos geométricos que se pueden ver como duales. Una instancia de uso de esa forma de ver esos conceptos duales se presenta en la forma de dos construcciones geométricas no triviales.
Sobre el concepto de dualidad
Dualidad significa doble perspectiva o doble significado o doble cara. Los siguientes ejemplos son clásicos en la ciencia: dualidad onda-partícula (toda la energía exhibe propiedades de onda y propiedades de partículas); dualidad voltaje-corriente; dualidad campos eléctricos-campos magnéticos.
En matemáticas se tiene el ejemplo clásico de los sólidos platónicos. Consideremos el cubo y los centros de cada una de sus caras. Uniendo mediante una arista los centros de cada par de caras adyacentes se obtiene un octaedro (el lector haría bien en detenerse a considerar esta transformación un tanto virtual). De esta manera, cambiando caras por vértices se obtiene otro sólido platónico. Es fácil convencerse de que efectuando la misma operación (de intercambio de caras por vértices) en el octaedro el resultado es el cubo. Si llamamos --como suele hacerse en matemáticas—primal al sólido de partida y dual al resultado del intercambio, la propiedad anterior se resume en la frase “el dual del dual es el primal.”
Otro ejemplo de dualidad se presenta en teoría de grafos. La representación de los sólidos platónicos (poliedros regulares) es un grafo plano. Con la misma idea de la transformación de los sólidos platónicos (intercambio de vértices y caras) se puede hablar del grafo dual de un grafo plano. Ver mi post http://www.matetam.com/blog/entradas-jmd/grafos-y-modelacion-relaciones
Recordemos, finalmente, la dualidad en teoría de conjuntos y lógica entre los cuantificadores existencial y universal (“existe un x” y “para todo x”) y la dualidad entre el or y el and lógicos. Una instancia de uso son las leyes de De Morgan: la afirmación primal “ninguna (de las propiedades) se cumple” es equivalente a esta otra (su dual): “es falso que alguna se cumpla”. Claramente la dualidad entre el or y el and (en lógica) se corresponde con la dualidad entre la unión y la intersección (en teoría de conjuntos) --tomando en cuenta que la negación (en lógica) se corresponde con la complementación (en teoría de conjuntos).
Se puede decir que la dualidad en matemáticas es una regla de correspondencia entre dos objetos matemáticos del mismo tipo. Y como la operación de pasar del primal al dual es reversible (el dual del dual es el primal), la correspondencia es uno a uno. (Aunque podrían existir objetos autoduales --como el tetraedro en la dualidad caras-vértices de los sólidos platónicos. Para una discusión más detallada de la dualidad en matemáticas ver http://en.wikipedia.org/wiki/Duality_(mathematics)
Bisectriz
La bisectriz de un ángulo MON se suele definir como el lugar geométrico de los puntos equidistantes de las rectas OM y ON. Esta idea corresponde a la imagen siguiente:
Con referencia a la figura, P es equidistante de las rectas OM y ON si y sólo si los ángulos MOP y PON son iguales --por el teorema del cateto y la hipotenusa y el criterio ALA de congruencia de triángulos.
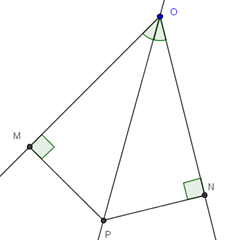
Pero hay otra forma de ver o conceptuar la bisectriz: la bisectriz es eje de simetría (eje de reflexión) de los lados del ángulo. Esta forma de de ver la bisectriz corresponde a la imagen siguiente:
Por definición, el punto N (en el lado ON del ángulo) es reflejo de M (en el lado OM del ángulo) en el espejo de la recta OP si y sólo si MN es perpendicular a la recta OP y ésta corta al segmento MN en su punto medio P. El lector no tendrá ningún problema para aportar la demostración del siguiente
Lema 1: el rayo OP es bisectriz del ángulo MON si y sólo si es eje de simetría de los lados del ángulo.
Punto medio
El punto medio de un segmento AB es el punto P del segmento que lo divide en dos segmentos iguales. Es decir, P es punto medio del segmento AB si y sólo si (por definición) AP=PB. Ahora bien, considerando esta definición con ojos de simetría, el punto medio es el centro de simetría de los extremos A,B del segmento.
Vistos de esta manera, la bisectriz y el punto medio son conceptos duales: El punto medio (la bisectriz) es centro (eje) de simetría de los extremos (lados) del segmento (ángulo).
Puesto que las diagonales de un paralelogramo se bisecan, es con frecuencia de gran utilidad el siguiente
Lema 2: El punto de intersección de las diagonales de un paralelogramo es centro de simetría de los lados opuestos.
Dos construcciones geométricas duales
Construcción 1: Dados una recta r y dos puntos M,N en lados opuestos de aquélla, construir las rectas m por M y n por N de tal manera que r sea bisectriz del ángulo que forman.
Construcción 2: Dadas dos rectas m,n no paralelas y un punto R entre ellas, construir los puntos M en m y N en n de tal manera que R sea punto medio del segmento MN
Los saluda
jmd
PD: Las soluciones y comentarios después...