Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que BP=PQ+QC
Sea $$BC$ el diametro de una semicirculo y sea $A$ el punto medio del semicirculo. Sea M un punto sobre el arco $AC$. Seam $P$ y $Q$ los pies de las perpendiculares desde $A$ y C a la linea $BM$, respectivamente.
Demustra que BP=PQ+QC
Aqui dejo la figura i un
Aqui dejo la figura i un traso super super auxiliar hhaahahah baje conganas haha a ta bn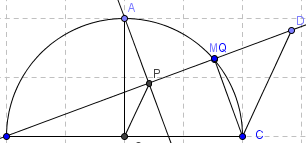
Primeramente, tenemos que
woooooooow. Primeros
woooooooow. Primeros comentarios ajenos a el problema que aun sigo bastante molesto por eso pro bueno que puedo hacer. asuuu tole qq tedioso lo isiste pero ai va la mia aber qq tal ;).
usando la figura del primer comentario (el mio), prolongo BM hasta un punto D tal que MD=MC entonces PD=PM+MC tons lo uniko qq falta es demostrar que BP=PD tonses iamemos O al centro de la semicircunferencia ii qe es punto medio de BC trazamos OP tons si demostramos que OP es paralela a CD por tales ia estaria tons tomamos el kuadrilatero OBAP ii que el angulo AOB=90=APB tons es ciclico => BAO=45=BPO donde eel resultado es klaro sino preguuuuntame hahahahhahah.
PD: que es eso de grupos le pongo crear y sale que crear problemas ii cosas asii???
Hola a ambos: Muy buenas
Hola a ambos:
Muy buenas demostraciones. Ambas usan una construcción auxiliar y usan ángulos para conlcuir la prueba. No creo que una sea mejor que la otra.
Por otro lado arbiter, pues eso de grupos es algo en lo que estamos pensando, pero por ahí en las pruebas lo dejamos puestos. Ya lo quitamos, cuando esté listo le explicaremos a todo mundo de qué se trata.
Saludos
hahahahah sobres carnal
hahahahah sobres carnal saludoos