Sea AB diametro de una semicircunferencia. Un punto M sobre la semicircunferencia y K un punto spbre AB. Una circunferencia con centro P pasa por A,M,K, y otra circunferencia de centro Q pasa por M,K,B. Demostrar que MPKQ es un cuadrilatero ciclico.
Sea AB diametro de una semicircunferencia. Un punto M sobre la semicircunferencia y K un punto spbre AB. Una circunferencia con centro P pasa por A,M,K, y otra circunferencia de centro Q pasa por M,K,B. Demostrar que MPKQ es un cuadrilatero ciclico.
El problema es muy sencillo;
El problema es muy sencillo; pero esta interesante porque de primera instancia se le encuentran muchas propiedades; haha poco utiles; y en cuanto a la solucion;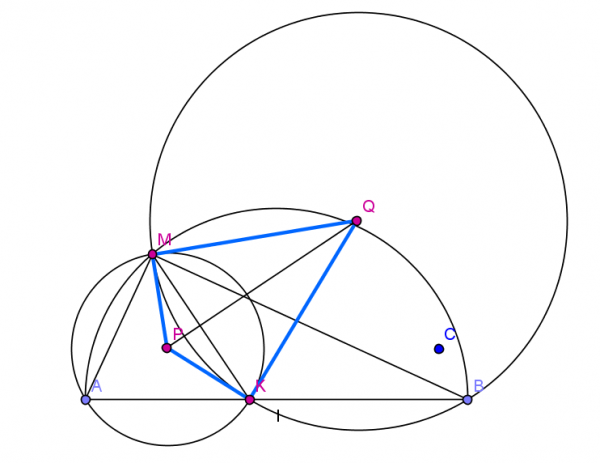
haha veo que salio un punto C de colaado; en fin; llamemos \alpha al angulo MAK y \beta al angulo MBK; sabemos que \alpha + \beta =90º ya que AKB es recto en K por tener como hipotenusa un diametro.
Ahora bien; <MPK=2 \alpha y <MQK=2 \beta ; como \alpha + \beta =90º; entonces 2( \alpha + \beta )=180º; con lo cual queda demostrado que MPKQ es ciclico ya que sus angulos opuestos suman 180º
hmm y una pregunta; ya
hmm y una pregunta; ya demostrado esto puedo afirmar que PMQ y PKQ son rectos verdad? porque PMQ y PKQ son congruentes entonces; sus angulos son iguales; y entonces son 180/2 cada uno ya lo habia demostrado; asi de una manera bieen geneal; haah creo qe me basaba en que PQ es bicectriz de los triangulos MPK y PQK; hah recuerdo que era algo geneal; pero lo hice ayer muy noche o hooy muy temprano y no se ni donde lo anote; qizás luego lo ponga; aunqe realmente ya qeda demostrado lo que nos pedia; haha
Pues si, efectivamente PQ es
Pues si, efectivamente PQ es bisectriz de los angulos en P y Q del cuadrilatero que piden demostrar es ciclico pero como lo demuestras sadhy? y si los triangulos son regtangulos pero da el por que , bueno se que debes saber el por que o almenos eso espero ahhaa por cierto yo no recuerdo ese problema del entrenamiento hahaha bueno pues sigue estudiando saludos!!