Publicaciones Recientes
Carta de Agradecimiento
Con el examen de la Etapa Regional han finalizado las fases en ciudades de la Olimpiada de Matemáticas en Tamaulipas. En días anteriores estuve un poco desconectado porque acompañé a los alumnos que participaron en la ONMAPS en la Ciudad de México, y por lo tanto no había tenido oportunidad de agradecer a todos los que nos han dado este gran apoyo en sus escuelas y municipios.
Prepárate para el Estatal con MaTeTaM (Números)
Para mejorar el desempeño de los competidores tamaulipecos en el Estatal, hemos decidido hacer una serie de posts compartiendo lo necesario para competir el 1 de julio. Esta primera entrada va orientada a aritmética o teoría de números, los temas necesarios son:
Sistema Decimal. Este tipo de problemas son ateoricos pues no se necesita saber mucho, son casi de lógica con un poco de combinatoria. No por eso son los más sencillos. Para participar en la olimpiada no necesitas saber más que los demás, si no saber usar lo que sabes.
Resultados de la OMM Tamaulipas etapa regional.
El dia de hoy, los seleccionados de la etapa municipal realizaron el segundo examen del proceso para pertenecer a la selección Tamaulipas 2016.
Presentaron en cuatro sedes: Reynosa,Victoria, El Mante y Madero. A continuación estan las actas de cada sede.
Los alumnos que aparezcan en estas actas estan seleccionados para participar en el concurso estatal a realizarse el 1 de julio de este año en las instalaciones de la UAM de Ciencias, Educación y Humanidades en Ciudad Victoria, Tamaulipas.
Los problemas los pueden consultar aquí mismo, ya estan arriba.
Saludos
Germán

Un dominó binario y marciano
Un dominó binario y marciano tiene fichas con un cero de un lado, y un uno del otro. Tenemos 6 fichas azules (las seis iguales), una roja y una verde. ¿De cuántas formas podemos hacer una fila con las ocho fichas si no debe haber dos fichas seguidas con cero juntos, pero sí puede haber dos unos seguidos, un cero seguido de un uno y un uno seguido de un cero?
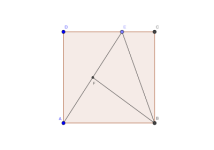
Medida de segmento para área 2016
Números chidos
Un número de tres cifras abc es chido si:
- Todas sus cifras son distintas y mayores a uno.
- Las fracciones bca,acb y bac son enteros.
a) ¿Cuál es el número chido más grande?
b) ¿Qué números chidos tienen la misma cifra en las centenas que el número encontrado en el inciso anterior?
El capicúa más cercano
Una sucesión de números mayores que 0 comienza con cualquier número y el siguiente será la resta entre el número anterior y el número capicúa más cercano que sea menor o igual al número. Por ejemplo 2016→14→3→0 Se observa que 14=2016 - 2002 ; 3 = 14 - 11 y 0 = 3 - 3. La sucesión termina cuando se llega a cero, en el ejemplo la sucesión tuvo cuatro términos ¿Cuál es el número más pequeño con el que puede iniciar la sucesión para que tenga exactamente 5 términos?
Elección de gatos de colores
En un barrio hay gatos de colores. Hay 15 rojos, 18 amarillos y 21 azules. En cada grupo de gatos de colores 2/3 son machos. ¿De cuántas maneras puedes tomar dos gatos del mismo color y el mismo sexo?
Juego de cartas con puntos de ataque
En un juego de cartas, cada una tiene un puntaje en defensa y ataque que cumple:
- Los puntajes son un número entero mayor que 0.
- Su puntaje en defensa es mayor al ataque.
- No hay dos cartas con el mismo ataque y la misma defensa.
Una carta A le gana a otra carta B si el ataque de A es mayor a la defensa de B. El poder de la carta es la cantidad de cartas a las que le gana. Tengo una carta cuya suma de puntajes de defensa y ataque es 50, ¿cuál es el máximo poder que podría tener esa carta?
Caminando en una escalera electríca
Una escalera eléctrica tarda 60 segundos en llevar a una persona del primer al segundo piso, la persona caminando tarda 90 segundos en subir esa misma escalera apagada. ¿Cuánto tarda esa persona en subir la escalera caminando y estando prendida?
