Publicaciones Recientes
Criterio para establecer cíclico con potencia de un punto
Si las rectas $AB,CD$ se cortan en $P$ y $PA\cdot{PB}=PC\cdot{PD}$, entonces los puntos $A,B,C,D$ pertenecen a una misma circunferencia. Demostrarlo.
Bisectriz, dos triángulos, circuncírculos, potencia...
La bisectriz del ángulo $B$ del triángulo $ABC$ corta a $CA$ en $D$. El circuncírculo del triángulo $BCD$ corta el lado $AB$ en $E$, y el circuncírculo del triángulo $ABD$ corta al lado $BC$ en $F$. Demostrar que $AE=CF$.
Dos homotecias en un trapecio
Las prolongaciones de los lados $AB$ y $CD$ de un trapecio se intersecan en $K$, y sus diagonales en $L$. Si $M,N$ son los puntos medios de de las bases, demostrar que los puntos $K,L,M,N$ están en una misma recta.
Paralelogramo de baricentros
Las diagonales de un cuadrilátero convexo dividen a éste en cuatro triángulos. Demostrar que sus baricentros forman un paralelogramo.
Problema sobre filas y columnas
Nuevamente vuelvo a pedir ayuda en esta excelente comunidad. El problema dice así:
En un tablero de $m\times n$ las filas se numeran de $1$ a $m$ y las columnas de $1$ a $n$. En cada casilla se escribe el resultado de multiplicar el numero de la fila por el de la columna. Luego se quitan las casillas interiores del rectángulo de $(m-2)\times (n-2)$, dejando un marco de ancho $1$. Las casillas de este marco se pintan alternadamente de blanco y negro. Si $m$ y $n$ son ambos impares, calcular la resta de la suma de los números de las casillas negras menos la suma de los números de las casillas blancas.
Espero que alguien me ayude. Muchas gracias.
Problem solving con homotecia
Como se sabe, la perspectiva transformacional en geometría permite el movimiento de las figuras y la transferencia de propiedades desde la figura a la figura transformada. De esta manera, la utilidad principal de esta perspectiva es la simplificación del problema, a la manera de un cambio de variable en álgebra. Voy a discutir en este post el caso de la homotecia (una transformación geométrica de muy bajo perfil en las matemáticas escolares) y su uso en el problem solving elemental a través de varios teoremas básicos de la geometría.
Cuatro problemas geométricos resueltos vía congruencia de triángulos
Uno de estos días abrimos en la Universidad (de Tamaulipas) un taller sabatino denominado “Taller de ciencia para jóvenes”. Acudieron a la convocatoria dos profesores de secundaria con 7 alumnos y un profesor jubilado.
El que esto escribe estuvo a cargo de la primera sesión con la intención de empezar a desarrollar el tema “Números complejos y Geometría Euclideana”, un tema que me parece muy productivo para la solución de problemas geométricos desde un punto de vista algebraico.
Dos problemas de construcción --con homotecia obligada
En un post anterior se plantearon dos problemas de construcción para ilustrar el poder de la homotecia en el problem solving de geometría. Aquí voy a resolverlos y a comentarlos, dado que --según creo-- merecen un post aparte. ("A: ¿Quieres decir que a la homotecia se le cocina aparte?" "JMD: Bueno, creo que lo que quiero decir es que el chiste no está en la homotecia misma, sino en saberla menear.")
Primer problema
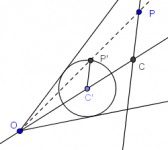
Sea dado un ángulo y un punto en su interior. Construir una circunferencia tangente a los lados del ángulo y que pase por el punto.
Solución y discusión del primer problema
Recíproco de Tales y el criterio LAL de semejanza
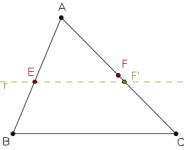
El teorema de Tales para triángulos es bastante intuitivo pues recurre a la conocida configuración de las paralelas y la transversal: si paralela a la base, entonces los segmentos son proporcionales.
Sin embargo, el recíproco de Tales nos dice que si los segmentos que determina una transversal en dos lados de un triángulo son proporcionales, entonces esa transversal es paralela al tercer lado.
Transformación geométrica de una circunferencia
Sean dadas dos circunferencias de radios diferentes y una afuera de la otra, y $H$ la intersección de sus tangentes exteriores comunes. Demostrar que para cualquier punto $A$ en una de las circunferencias, existe un punto $B$ en la otra de tal manera que $HA\cdot{HB}=HP\cdot{HQ}$, donde $P,Q$ son los puntos de tangencia de una de las tangentes comunes.
