Publicaciones Recientes
Criterios de congruencia como postulados
Los criterios o principios de congruencia nos dicen cómo determinar si dos triángulos son congruentes sin necesidad de verificar las seis igualdades entre lados y ángulos correspondientes.
Criterio LAL (Lado-ángulo-lado). Es posiblemente el criterio de congruencia más básico, este criterio nos dice que si, en una correspondencia de triángulos, dos lados de uno y el ángulo comprendido entre ellos son iguales a sus correspondientes elementos en el otro, entonces los dos triángulos son congruentes.
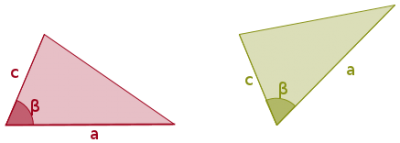
Congruencia de triángulos como noción intuitiva y su formalización
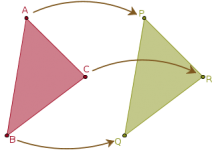
Después de haber descubierto el hecho de que dos triángulos son congruentes (iguales) es conveniente poner sus vértices en correspondencia.

El triángulo como configuración de puntos y rectas
Como se sabe, hay diversas clasificaciones de triángulos que dan cuenta de su diversidad de forma: de acuerdo a la medida de sus ángulos pueden ser obtusángulos, rectángulos, acutángulos; de acuerdo a la relación de las medidas de sus lados pueden ser equiláteros, isósceles, escalenos. Es por eso que una noción previa a la definición de congruencia de triángulos es la de corres
Igualdad y congruencia
El concepto de congruencia está emparentado con el de igualdad y se espera que el aprendiz la conozca ya sea por su significado intuitivo a partir del lenguaje natural, o bien a través de su uso en la aritmética.
Es costumbre que en geometría se hable de congruencia en vez de igualdad. Por ejemplo dos segmentos son congruentes si y sólo si tienen la misma medida –y lo mismo es cierto para ángulos. Pero en el caso de dos triángulos la definición es más complicada pues no hay una medida (número) que defina a un triángulo.

Uno de cuadráticas
El cuadrado de un número disminuido en 924 es igual 20 veces dicho número. ¿Cuál es ese número? (Genera uno similar.)
Dos en uno
La suma de dos números es 36 (variante: 750) y su producto es 243 (variante: 78125). Encuentra los números. ¿Podrías plantear uno con la misma estructura?
Lourdes y su madre
La edad de Lourdes es un divisor primo (y no es 3) de la edad de su madre y ésta tenía 39 cuando aquélla nació . ¿Cuántos años tienen?

Perico de los Palotes
Un ejidatario de Soto le vende pericos y cotorras a un traficante que los lleva a USA. Este año le vendió 7 pájaros verdes: los pericos a 150 dólares y las cotorras a 100. Si el traficante le pagó 900 dólares ¿cuántos pericos le compró?

Life in plastic, it's fantastic
Teresa, la madre de Kira, es una chica barbie de la ciudad (étnica, al igual que su hija, y ya de cierta edad). En sus tiempos coleccionó muñecas Barbie de Mattel (el calificativo es importante, es decir, no son piratas). Kira cuenta que su madre las tiene todas y desea plantear a los usuarios de MaTeTaM el siguiente problema: si vendiera 30 le quedarían el triple que si vendiera 100 ¿cuántas barbies tiene la mamá de Kira?

Adopta un abuelito
El chico fresa es también un filántropo. De acuerdo a la política "adopta un abuelito" del gobernador, decidió contribuir a la felicidad de los 5 adultos mayores de su manzana. Deseando que disfrutaran de los placeres de la realidad virtual, les regaló sus juegos de video que compró el año pasado en McAllen (este año se casa y siente que su adicción al Xbox debe quedar en el pasado). Al primero le regaló la mitad de ellos menos 8; al segundo, la mitad de los restantes menos 8; al tercero, la mitad de los que le quedaban menos 8, y lo mismo hizo con el cuarto. Le quedaron 20 y se los dio al quinto adulto mayor de su manzana.

