Publicaciones Recientes
El promedio es el centro
El promedio de dos números reales está exactamente a la mitad del camino entre ellos. Demostrarlo.
Un 2011, ya no digamos feliz, sino al menos bien administrado... por Egidio Torre Cantú
(Son los mejores deseos de MaTeTaM para este año y los siguientes... por lo menos 6 --para las Matemáticas en Tamaulipas.)
En este post de bienvenida al 2011, el cual es de matemáticas sólo de manera indirecta, reconozco como muy buenas las primeras jugadas del ingeniero Egidio Torre Cantú (el flamante gobernador de Tamaulipas), en particular el nombramiento de Diódoro Guerra Rodríguez como secretario de educación en Tamaulipas.
Calendario dodecaédrico 2011 con origami
Aquí está el calendario dodecaédrico 2011 con origami. Tiene un mejor diseño y marcamos los días festivos. Descarga, imprime y arma, es muy fácil. ¡Esperamos que les guste!
Feliz Año Nuevo
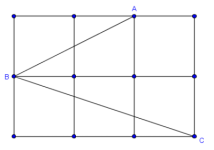
Con trigonometría (a veces) la creatividad es innecesaria
Hablando en general, la solución de un problema de geometría exige cierta creatividad. Ésta, con frecuencia, consiste en ver el problema de otra forma. Por ejemplo, ampliando el contexto mediante un trazo auxiliar.
Se trata del fenómeno del framing el cual he abordado en otros posts en MaTeTaM. Framing se traduce como encuadre o enmarcamiento, como cuando se le pone el marco a una fotografía o pintura. Así pues, la creatividad, con frecuencia, consiste en poner al problema en un marco adecuado.
La reina ha muerto. ¡Viva la reina!
(Una Gaga (g) en rápido crecimiento, y rompiendo con todos los clichés, ha destronado en 2010 a Madonna (m) --una ex-reyna del pop ya en lento decaimiento.) Dentro de 4 años m tendrá el doble de la edad de g y la diferencia de sus edades es múltiplo de 7. Calcular éstas si se sabe además que g es mayor de edad y m todavía no es adulto en plenitud.
Fan de Lady Gaga
Camila, la princesa de la prepa, se reunió con tres de sus amigas y les regaló copias en CD del album más premiado del año (The Fame Monster, edición de lujo). A la primera le obsequió la mitad de las que traía en su mochila más dos, a la segunda la mitad de los que le quedaban más dos, y a la tercera la mitad de los que le quedaban más dos. Después del reparto le quedó una copia para ella. ¿Cuántas copias de The Fame Monster traía Camila en su mochila?

Pequeño problema de teoría de números
Señores maestros y estudiantes, tengo un pequeño problema que me está quitando el sueño. Lo coloco a continuación:
"Un grupo de personas es tal que contadas de a en a, sobran m, y contadas de b en b faltan n. Halla el número de personas en función de a, b, m y n"
Ojalá pueda alguien ayudarme.
Gracias de antemano.
Línea de Euler
Demuestra que, para un triángulo no equilátero, el circuncentro, el gravicentro y el ortocentro están sobre una misma recta.
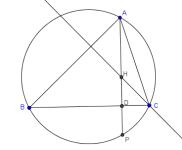
Ejercicio con baricentro y circuncentro
En la figura se muestra un triángulo ABC y su circuncírculo. El segmento que va desde el circuncentro O (concurrencia de mediatrices) al gravicentro G (concurrencia de medianas) se ha prolongado hasta cortar a la altura AD en H.
Demostrar:
- (a) Los triángulos OMG y HAG son semejantes
- (b) El segmento GH mide el doble que el OG
- (c) En H concurren las tres alturas
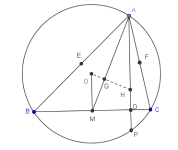
Ejercicio con ortocentro
En la figura, H es la intersección de las alturas, y la altura AD del triángulo ABC se ha prolongado hasta cortar el circuncírculo en P.
Demostrar:
- (a) El triángulo HBC es isósceles
- (b) La recta BC es mediatriz de HP
- (c) Los puntos H y P son simétricos respecto al lado BC