Publicaciones Recientes
Ángulo postgiro
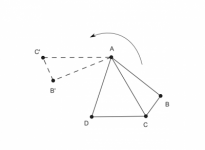
2.2. Sea ABCD un cuadrilátero que cumple: AB=AD,AC=BC+CD y los ángulos ABC y CDA suman 180 grados. El triángulo ABC se gira con centro en A formando el triángulo AB'C', como se muestra en la figura, hasta que el punto B' coincida con D, formándose el triángulo ADC'. Encuentra la medida del ángulo ACC'.
Huevos y chilaquiles en buffet
2.1. Cierto día en el restaurante La Cascada prepararon para el buffet de desayuno una charola de cada uno de los siguientes siete platillos: huevos con tocino, frijoles con queso, huevos con jamón, huevos a la mexicana, chilaquiles rojos, chilaquiles con huevo y chilaquiles verdes. Se le ordena al mesero acomodar las charolas de los platillos, alineadas en la barra, de forma tal que las que contengan huevo queden juntas y que las que contengan chilaquiles queden juntas.
Isósceles inscrito en acutángulo
1.6. Sean ABC un triángulo acutángulo, H su ortocentro y M el punto medio de BC. La perpendicular a MH por H corta a AB en L y a AC en N. Demuestra que LH=HN.
Ordenar los superhéroes
1.5. Heberto tiene en su colección de figuras de acción de superhéroes dos Hulk, dos Superman,dos Ironman, dos Batman que quiere acomodar en línea sobre una repisa. Quiere que entre cada dos superhéroes iguales haya una cantidad diferente de figuras. Por ejemplo, si hay tres figuras entre los dos Hulk, no podría haber tres figuras entre los dos Batman. De cuántas maneras diferentes puede hacer esto?
La lista de Julio
1.4. Julio hace una lista con los números que cumplen las siguientes condiciones:
--El número es de ocho cifras, todas diferentes.
--Es múltiplo de 8.
--Cada dos cifras adyacentes en el número forman un nuevo número que es múltiplo de 7 o de 13, aunque no necesariamente todos múltiplos del mismo número.
Encuentra los números de la lista de Julio.
Razón de áreas en un hexágono
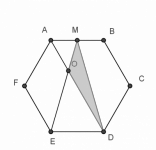
1.3. Sean ABCDEF un hexágono regular y M el punto medio del lado AB. Si O es el punto donde se cruzan los segmentos AD y ME ¿qué parte del área del hexágono es el área del triángulo OMD?
Números mazatlecos
1.2. Se dice que un número de cuatro cifras diferentes entre sí y distintas de cero es Mazatleco si al eliminar la mayor y la menor de las cifras, las dos restantes suman 10. ¿Cuántos números Mazatlecos hay?
Llevar o no llevar: that's the question
1.1. Se forman tres números enteros de tres cifras, abc,def,ghi, donde cada letra representa un dígito del 1 al 9 sin que se repitan. Si la suma de los tres números termina en 65 ¿cuál es el valor de dicha suma?
XIV ONMAPS (segundo día)
2.1. Cierto día en el restaurante La Cascada prepararon para el buffet de desayuno una charola de cada uno de los siguientes siete platillos: huevos con tocino, frijoles con queso, huevos con jamón, huevos a la mexicana, chilaquiles rojos, chilaquiles con huevo y chilaquiles verdes. Se le ordena al mesero acomodar las charolas de los platillos, alineadas en la barra, de fprma tal que las que contengan huevo queden juntas y que las que contengan chilaquiles queden juntas. ¿De cuántas maneras diferentes pueden ordenarse lascharolas en la barra (de izquierda a derecha)?

XIV ONMAPS (primer día)
Esta semana se realizó en Mazatlán la XIV Olimpiada de Matemáticas para Alumnos de Primaria y Secundaria (ONMAPS). El lunes 19 los concursantes resolvieron la primera parte, y el martes la segunda. En cada una, el examen consistió de 6 problemas y los concursantes debían resolver 3 según su nivel o categoría:
Primaria resolvió los problemas 1,2,3.
Primer grado los problemas 2,3,4.
Segundo grado los problemas 3,4,5.
Tercer grado los problemas 4,5,6.
Los problemas del primer día son los siguientes:

