En esta cuarta lección presento, a través de la regla distributiva, algunos resultados básicos de la combinatoria. En este sentido es una continuación de la lección de álgebra. A través del principio multiplicativo se derivan las fórmulas de las permutaciones y de las combinaciones o coeficientes binomiales.
Principios combinatorios en la expansión de productos
De acuerdo a la regla distributiva, en la expansión de un producto de polinomios (a+b+c)(d+e+f+g) se toman todos los productos posibles tomando un término de cada paréntesis: ad+ae+...+cf+cg.
Cada uno de los términos de la expansión está formado por una literal del primer paréntesis multiplicada por una del segundo. El primer factor lo puedo elegir de 3 formas y el segundo de 4. ¿Cuántos términos hay en la expansión? Respuesta: 3×4=12. ¿Y si hubiera m literales en el primer paréntesis y n en el segundo? Respuesta: m×n. Es casi obvio que no es necesario contar los términos de la expansión.
Si pensamos el producto de polinomios como tabla, se hace evidente que podemos contar sin contar:
| d | e | f | g | |
|---|---|---|---|---|
| a | ad | ae | af | ag |
| b | bd | be | bf | bg |
| c | cd | ce | cf | cg |
Esta forma de contar sin contar es básica en combinatoria y se le llama
Principio multiplicativo: si una decisión puede descomponerse en dos etapas con m opciones en la primera y n en la segunda, entonces la decisión se puede tomar de mn formas.
Es todavía más evidente si representamos la situación con un diagrama de árbol
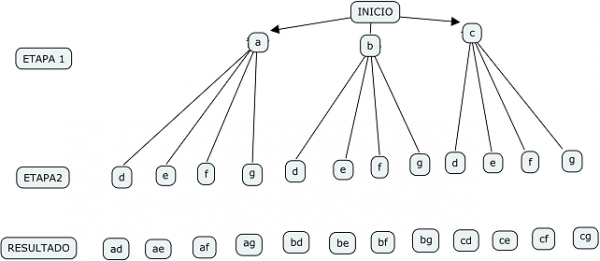
Interpretación combinatoria de la expansión de productos
Si interpretamos los paréntesis como conjuntos (con las literales como sus elementos), en el ejemplo anterior (a+b+c) representaría el conjunto {a,b,c}. Así que, en la expansión del producto, los términos están formados por un elemento del primer conjunto multiplicado por un elemento del segundo.
De esta manera, los términos de la expansión se pueden interpretar de nuevo como conjuntos de dos elementos. Por ejemplo, el término cf se interpretaría como el conjunto {c,f}. Es decir, los términos de la expansión son conjuntos: en el ejemplo, conjuntos de dos elementos, un elemento tomado del conjunto {a,b,c} y el otro elemento tomado de {d,e,f,g}.
Imaginemos ahora que el binomio (1+a) lo interpretamos como el conjunto que tiene únicamente el elemento a, y que el 1 nos sirve solamente como mecanismo de decisión: no elegir el elemento a en el momento de expandir un producto. En esta interpretación, los términos de la expansión de (1+a)(1+b)(1+c) son todos los subconjuntos de {a,b,c}: 1+b+c+ab+bc+ca+abc. El 1 se interpreta como el conjunto vacío.
Esta interpretación deriva del hecho bien conocido de que, al elegir los subconjuntos, puedo hacerlo en forma secuencial: en la etapa i decido si elijo el elemento i (para pertenecer al subconjunto) o bien no lo elijo.
De esta manera, la expansión de un producto del tipo
(1+a)(1+b)(1+c)(1+d) es equivalente, bajo esa interpretación, a enumerar todos los subconjuntos de {a,b,c,d}. Es decir,
1+a+b+c+d+ab+ac+ad+bc+bd+cd+abc+abd+acd+bcd+abcd
Quizá el mejor truco jamás inventado en matemáticas elementales es el siguiente: para agrupar los subconjuntos (términos de la expansión) por tamaño, multiplicamos por una x a las literales (elementos) de los binomios. De esta manera, el exponente de la x en la expansión sirve como contador --de las veces que se eligió un elemento (una literal) en la expansión utilizando la regla distributiva.
(1+ax)(1+bx)(1+cx)=1+(a+b+c)x+(ab+bc+ca)x2+(abc)x3
Y si nos interesara saber (como es lo usual) solamente cuántos subconjuntos de cada tamaño hay, basta con hacer cada literal igual a 1 (a=b=c=1) :
(1+x)(1+x)(1+x)=1+3x+3x2+x3
¡Pero esto es precisamente la expansión del binomio de Newton!
Coeficientes binomiales y modelación algebraica de la elección
Debería ser claro entonces que el coeficiente del término k de la expansión de un binomio (elevado a una potencia entera positiva n) cuenta los subconjuntos de tamaño k tomados de un conjunto de tamaño n. En otras palabras, contesta a la pregunta ¿de cuántas formas se pueden elegir k elementos de un conjunto de tamaño n?
Es decir, el coeficiente C(n,k) de xk en la expansión del binomio de Newton (1+x)n cuenta el número de subconjuntos de tamaño k tomados de un conjunto de tamaño n.
Cada uno de los binomios (1+x) se asocia con uno de los elementos del conjunto, digamos, {1,2,3,…,n}, en el sentido de una decisión:
1, no lo elijo
x, sí lo elijo
O, mejor,
1=x0, lo elijo cero veces;
x1, lo elijo una vez.
Esta última interpretación deja abierta la posibilidad de elegir más de un objeto de un mismo tipo como es el caso de muchos problemas combinatorios. (Piense el lector en el pan de la panadería: 2 conchas, 3 hojaldrados, etc.)
Si tenemos objetos de dos tipos, peras y manzanas por ejemplo ¿de cuántas formas puedo elegir 7 frutas --bajo la condición de elegir al menos una de cada tipo y solamente hay 6 peras y 6 manzanas?
El modelo algebraico para contar las posibilidades asocia a cada tipo de fruta el polinomio (x+x2+…+x6), y el problema se reduce a determinar el coeficiente de x7 en la expansión de (x+x2+…+x6)2.
Este mismo modelo sirve para el siguiente problema: ¿de cuántas formas se puede obtener la suma 7 en el lanzamiento de dos dados? (Los tipos de objeto aquí son los puntos del primer dado y los puntos del segundo.)
Binomio de Newton: (1+x)n
(1+x)0=1(1+x)1=1+x(1+x)2=1+2x+x2(1+x)3=1+3x+3x2+x3(x+y)4=1+4x+6x2+4x3+x4(x+y)5=1+5x+10x2+10x3+5x4+x5
Si atendemos solamente a los coeficientes de la expansión del binomio de Newton, debería ser claro que éstos forman un arreglo triangular denominado Triángulo de Pascal. Nótese que cada número es la suma de los dos números inmediatamente superiores:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
El Triángulo de Pascal puede también organizarse como tabla
| n/k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | |||||||
| 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 1 | |||||
| 3 | 1 | 3 | 3 | 1 | ||||
| 4 | 1 | 4 | 6 | 4 | 1 | |||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | ||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | |
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
| etc |
En general, la regla de formación de los coeficientes depende de dos variables: el exponente n (la fila en la tabla) y la posición k (la columna) del coeficiente en la expansión. La notación C(n,k) se usa para referirse al coeficiente en la posición k-ésima en la expansión de (1+x)n.
Dado un exponente n, queda definido un renglón o fila del arreglo (el renglón n). El coeficiente en la columna k, es:
C(n,k)=C(n–1,k–1)+C(n–1,k)
Es decir, para obtener el (n,k) se suman el de arriba a la izquierda y el de exactamente arriba.
Para destacar los coeficientes binomiales, se expande (1+x)n:
(1+x)n=C(n,0)+C(n,1)x+C(n,2)x2+...+C(n,k)xk+...+C(n,n)xn
Más adelante se determinará la fórmula de C(n,k) a partir del principio multiplicativo. Por lo pronto, sepa el lector que es la siguiente:
C(n,k)=n(n−1)(n−2)...(n−k+1)k(k−1)(k−2)...1
con k≥0 , C(n,0)=1
Notemos que el numerador y el denominador tienen ambos k factores. Como ejercicio, el lector puede verificar la fórmula para los coeficientes C(n,k) desarrollando el binomio para n=2,3,4,5.
Una regla útil para el arranque: (x+y)n=xn+nxn−1y+⋯
(Es decir, el arranque ya está garantizado: “el primer término a la n, más n veces...”)
Ejercicios:
1. El cuarto término del binomio (x+2)8
2. El coeficiente del séptimo término del binomio (−3+x)10
3.El tercer término del binomio (3x+4y)5
Aplicaciones elementales del principio multiplicativo
De acuerdo al principio multiplicativo, con las letras de la palabra AMOR se pueden formar 4×3×2×1=24 palabras del mismo tamaño. Y esto porque para la primera letra existen 4 posibilidades, digamos que sea la R, y una vez elegida la primera, para la segunda hay 3 posibilidades (A,M,O), etc.
Este problema de ordenar n objetos distintos en todas las formas posibles se le llama número de permutaciones de n objetos y el total de posibilidades se denota con n! (que debe leerse como n factorial o factorial de n). Y se calcula mediante la fórmula n!=n⋅(n−1)⋅(n−2)⋯⋅2⋅1.
Nota: Cada una de las ordenaciones de n objetos distintos es una permutación de esos objetos; por ejemplo, las permutaciones de los números 1,2,3 son 123,132,213,231,312,321.
También por el principio multiplicativo se puede responder a la pregunta ¿cuántas palabras de dos letras diferentes se pueden formar con las de la palabra AMOR? La respuesta es 12, pues la primera letra puede ser cualquiera de las 4, pero para la segunda solamente se tienen 3 posibilidades.
Para obtener la fórmula para el número de subconjuntos de tamaño k con elementos de {1,2,3,…,n}, hay que tomar en cuenta que cada uno de esos subconjuntos corresponde a k! órdenes posibles de sus elementos.
De aquí que todos los órdenes posibles de longitud k con los elementos de {1,2,3,…,n} se pueden clasificar en C(n,k) grupos (uno por cada subconjunto), cada grupo con k! órdenes.
Así que, de nuevo por el principio multiplicativo, k!C(n,k)=n(n−1)…(n−k+1). De aquí la fórmuala dada más arriba.
Instancias de uso combinatorio del binomio de Newton
1. En una librería me gustaron 7 libros de matemáticas. Sólo quiero comprar 4. ¿Cuántas posibilidades hay de elegir 4 libros distintos?
Solución:
Claramente se trata aquí de calcular el número de subconjuntos de tamaño 4, tomados de un conjunto de tamaño 7. La respuesta es entonces C(7,4), el coeficiente de x4 en la expansión de (1+x)7. En el triángulo de Pascal es el número 35, ubicado en el renglón 7 y columna 4.
2. Una identidad fundamental: C(n,k)=C(n,n−k)
En el triángulo de Pascal se puede observar la simetría de los coeficientes en el renglón n. En la interpretación combinatoria de los coeficientes --del binomio de Newton-- como número de subconjuntos de tamaño k, tal simetría se explica argumentando que al elegir un subconjunto de tamaño k, implícitamente hemos elegido también uno de tamaño n−k. (En el ejemplo de la librería, compré 4 libros de los 7 que me habían gustado; pero también elegí no comprar los 3 que se quedaron sobre la mesa.)
Matemáticamente, el argumento es de correspondencia uno a uno entre los subconjuntos de tamaño k y los subconjuntos de tamaño n−k: a cada subconjunto A de S lo pongo en correspondencia con el subconjunto complementario S−A --los elementos de S que no están en A .
3. La suma de los coeficientes del k-ésimo término y del (k+1)-ésimo término del desarrollo de (1+x)n es igual al coeficiente (k+1)-ésimo del desarrollo de (1+x)n+1. En otras palabras:
C(n,k)+C(n,k+1)=C(n+1,k+1)
Esta fórmula se puede obtener mediante el siguiente argumento (o interpretación): los subconjuntos de tamaño k+1 de {1,2,3,…,n,n+1} se pueden separar en dos grupos: los que contienen el elemento n+1 y los que no lo contienen. Los si contienen el n+1 son tantos como C(n,k) --pues los restantes k elementos se eligen del conjunto {1,2,3,…,n}; los que no contienen al n+1 son C(n,k+1). De ahí el resulltado.
Identidades combinatorias con binomio de Newton
1. Consideremos la expansión de (1+x)n :
(1+x)n=C(n,0)+C(n,1)x+C(n,2)x2+...+C(n,k)xk+...+C(n,n)xn
Si hacemos x=1, se obtiene la identidad:
2n=C(n,0)+C(n,1)+C(n,2)+...+C(n,k)+...+C(n,n)
Esta identidad tiene la siguiente interpretación combinatoria: el número de subconjuntos de un conjunto de tamaño n es 2n.
Si hacemos x=−1, se obtiene la identidad:
C(n,0)−C(n,1)+C(n,2)−...+(−1)kC(n,k)+...+(−1)nC(n,n)=0
Esta identidad tiene la interpretación combinatoria siguiente: el número de subconjuntos de tamaño par (de un conjunto de tamaño n) es igual al número de subconjuntos de tamaño impar.
Si hacemos x=2, se obtiene la identidad:
C(n,0)+2C(n,1)+4C(n,2)+8C(n,3)+...+2nC(n,n)=3n
2. ¿De cuántas formas se puede dividir un grupo de X+Y objetos en dos grupos, uno de X y otro de Y objetos?
3. Verificar que en todas las filas del Triángulo de Pascal la suma de los números en posiciones impares es igual a la suma de los números en posiciones pares. Interpretar el hecho en términos de subconjuntos.
4. Se rotulan 9 objetos con A,B,C,D,E,F,G,H,I. ¿De cuántas maneras se pueden distribuir estos objetos en 3 bolsas: una de 2, una de 3 y otra de 4?
5. Supongamos que un conjunto de n objetos se ha distribuido en 3 grupos de p,q y r elementos, con n=p+q+r ¿De cuántas maneras se pueden formar los 3 grupos?
6. Hay n objetos diferentes en una circunferencia. Demostrar que la cantidad de maneras en las que se puede elegir 3 elementos de entre ellos de forma que no haya 3 adyacentes es 1/6n(n−4)(n−5)
7. La cantidad de maneras de ubicar n letras distintas en una fila es n!
8. Demostrar que la cantidad de "oraciones" de r "palabras" que se pueden formar con n letras es
n!(n−1)!(n−r)!(r−1)!
Divisibilidad con binomio de Newton
(i) 539–239 es divisible entre 3.
Demostración: 539=(3+2)39=339+39(3)38(2)+...+39(3)238+239
Entonces, todos los sumandos son múltiplos de 3 excepto el último. Pero éste se elimina con −239.
(ii) 299+399 es divisible entre 5.
Demostración: En este caso, 299+399=(5–3)99+399 y de nuevo se ve que los sumandos de la expansión son todos múltiplos de 5 excepto el último. Pero éste se cancela.
(iii) 298+398 NO es divisible entre 5.
Demostración: La diferencia con el problema anterior es que aquí el último término de la expansión de (5–3)98 es (−3)98=398 y no puede cancelarse con 398.
(iv) 299+399+499+599 es divisible entre 7.
Demostración: Con las soluciones ya vistas, se deja al lector su solución. Baste decir que la expresión puede ponerse como
(7–5)99+(7–4)99+499+599
(v) 299−499−799+999 es divisible entrer 10.
(vi) Hallar una fórmula para calcular el valor de:
(a) 1+x+x2+...+xn para cualquier valor entero positivo de n
(b) 1−x+x2−...+xn para cualquier valor entero positivo e impar de n.
(vii) Explicar por qué, para cualesquiera a y b enteros,
(a) (a+b)3–a3–b3 es divisible entre 3.
(b) (a+b)5–a5–b5 es divisible entre 5.
(c) (a+b)7–a7–b7 es divisible entre 7.
Los saluda
jmd
