Junio 2011
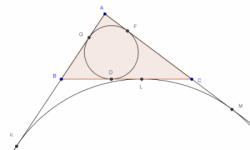
Problem solving con homotecia
Como se sabe, la perspectiva transformacional en geometría permite el movimiento de las figuras y la transferencia de propiedades desde la figura a la figura transformada. De esta manera, la utilidad principal de esta perspectiva es la simplificación del problema, a la manera de un cambio de variable en álgebra. Voy a discutir en este post el caso de la homotecia (una transformación geométrica de muy bajo perfil en las matemáticas escolares) y su uso en el problem solving elemental a través de varios teoremas básicos de la geometría.
Un problema clásico de homotecia
Durante el año 2009, al final de uno de los entrenamientos de la OMM Delegación Tamaulipas, Jesús Rodríguez Viorato le planteó el siguiente problema a Luis Brandon --el líder de la selección 2009:
El incírculo de un triángulo $ABC$, es tangente en $D$ al lado $BC$ y $DM$ es un diámetro. El rayo $AM$ corta en $F$ el lado $BC$. Demostrar que $BD=CF$.
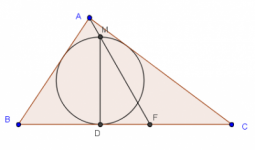
Discusión sobre incírculos y excírculos
Voy a discutir en este post algunos conceptos relacionados con las circunferencias incrita y exinscrita. Dichos conceptos forman un todo y conviene aprenderlos en paquete --es muchísimo más fácil retenerlos en la memoria y comprenderlos si se aprenden en sus interconexiones.
Se trata de los conceptos de semiperímetro --en el contexto de ciertas simetrías entre las longitudes de las tangentes de circuncírculo y excírculos--, el concepto de puntos isotómicos, y el de los puntos de Gergonne y Nagel --como ejemplo de puntos conjugados isotómicos.