Básico

Verónica tiene más faldas que blusas y afirma que puede vestirse todos los días de un año normal usando un conjunto falda-blusa sin repetir. Anahí le comenta que si fuera un año bisiesto esto no podría hacerlo. Hallar el número de faldas y blusas que tiene Verónica si se sabe que tiene más de una blusa.

Xavier tiene el mismo número de hermanas que de hermanos. Su hermana Yara tiene el doble de hermanos que de hermanas. ¿Cuántos hermanos y cuántas hermanas hay en esta familia?

1. Se desea cercar un terreno de 2000m², expresa una ecuación que defina la cantidad de cerco en función de su lado de mayor longitud. Nota: Es un terreno rectangular.

2. Expresa el área de una caja con base cuadrangular si tiene un volumen de 16m² expresala en función de la longitud de su altura.

3.Se desea construir un cilindro de 40 cm³, expresa el área del cilindro en función de su radio.

Con cuadrados de lado 1 se forma en cada etapa una figura en forma de escalera siguiendo el patron del dibujo 

Por ejemplo, la primera etapa utiliza un cuadrado, la segunda utiliza 5. Determine la última etapa para la cual la figura correspondiente utiliza menos de 2014 cuadrados.

Sea  un trapecio $ABCD$ de bases $AB$  y $CD$ , inscrito en una circunferencia de radio $O$. Sea $P$ la intersección de las rectas $AD$ y $BC$ . Una circunferencia por $O$ y $P$  corta a los segmentos $BC$ y $AD$ en puntos interiores $F$ y $G$ respectivamente. Muestre que $BF=DG$ .

2.G. Sean ABC un triángulo isósceles con AB=AC, y P en AB y Q en AC puntostales que AP=CQ. Sea O la intersección de las mediatrices de PQ y AC.

a) Demostrar que APO y CQO son triángulos congruentes.
b) Demostrar que APOQ es un cuadrilátero cíclico.
c) Demostrar que AO es bisectriz del ángulo BAC.

(Nota: Para el inciso b puedes usar el resultado del a (sin demostración); para el cpuedes usar los resultados de a y b.)

1.C. ¿Cuántos números del 10 al 99 son tales que sus dígitos están en orden decreciente? Nota: 31 cumple pero no el 44 ni el 56.

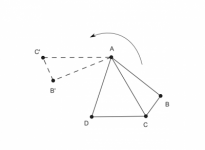
2.2. Sea ABCD un cuadrilátero que cumple: AB=AD,AC=BC+CD y los ángulos ABC y CDA suman 180 grados. El triángulo ABC se gira con centro en A formando el triángulo AB'C', como se muestra en la figura, hasta que el punto B' coincida con D, formándose el triángulo ADC'. Encuentra la medida del ángulo ACC'.

2.1. Cierto día en el restaurante La Cascada prepararon para el buffet de desayuno una charola de cada uno de los siguientes siete platillos: huevos con tocino, frijoles con queso, huevos con jamón, huevos a la mexicana, chilaquiles rojos, chilaquiles con huevo y chilaquiles verdes. Se le ordena al mesero acomodar las charolas de los platillos, alineadas en la barra, de forma tal que las que contengan huevo queden juntas y que las que contengan chilaquiles queden juntas.

1.5.  Heberto tiene en su colección de figuras de acción de superhéroes dos Hulk, dos Superman,dos Ironman, dos Batman que quiere acomodar en línea sobre una repisa. Quiere que entre cada dos superhéroes iguales haya una cantidad diferente de figuras. Por ejemplo, si hay tres figuras entre los dos Hulk, no podría haber tres figuras entre los dos Batman. De cuántas maneras diferentes puede hacer esto?