Intermedio

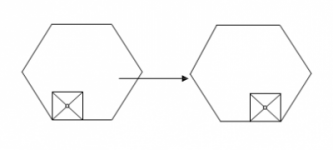
En la esquina inferior izquierda de un hexágono regular de lado 4 metros se coloca un cuadrado de lado 2 metros, tal y como se observa en la parte izquierda de la figura.

El cuadrado “rueda” (sin deslizarse) sobre los lados del hexágono y por la parte interior de éste, girando en el sentido inverso de las agujas del reloj y manteniendo siempre un vértice apoyado en un lado del hexágono (el primer movimiento aparece en la figura). Cuando el punto $P$ --que es la intersección de las diagonales del cuadrado-- vuelve a su posición inicial ¿Cuántos metros ha recorrido?

Encontrar el residuo de dividir entre 5 el número $N= 1 + 4 + 4^2 + 4^3 + 4^4 +\ldots+4^{2007}$

El abuelo reparte 2007 monedas entre sus nueve nietos (digamos A, B, C, D, E, F, G, H e I) de la siguiente manera: Los sienta alrededor de una mesa en el orden de sus nombres y va entregando en ese mismo orden una moneda a cada uno; empieza con A y, al completar la vuelta, la siguiente vuelta comienza con el último, es decir, le entrega una más a I y continúa con A; entregando moneda por moneda, termina la siguiente vuelta con H, le entrega su moneda y con él mismo inicia la siguiente vuelta. Procede de esta manera hasta agotar todas las 2007 monedas. ¿Cuántas monedas le tocaron a cada nieto? ¿A cuál de los nietos le entregó la última moneda?

En un cuadrilátero $ABCD$, con ángulos interiores menores a 180 grados, los lados $AB, BC$ y $CD$ son iguales. También sabemos que $AD = AC = BD$. Encuentra la medida del ángulo $ABC$.

Para cualquier número natural $n$ se dice que su origen se calcula multiplicando sus cifras, después las cifras del resultado, y así sucesivamente hasta llegar a un número de una sola cifra. Por ejemplo, el origen del 149 es el 8, ya que $149\rightarrow36\rightarrow 18\rightarrow 8$; y el origen del 5486 es el 0, ya que $5486\rightarrow 960\rightarrow 0$. Encuentra la suma de todos los números de dos o más cifras distintas, tales que su origen sea un número impar.

En la figura, el rectángulo tiene lados de 10 cm. y de 8 cm. y éstos se han dividido como se indica de manera que al unir los puntos de división se forma un paralelogramo (ojo sus ángulos no son rectos). Calcula la distancia entre los lados paralelos más pequeños, indicada con la línea d.

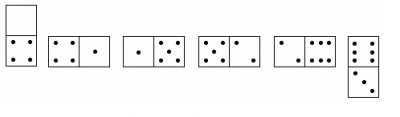
Como se ve en la ilustración se han jugado seis fichas de dominó. De acuerdo a las reglas del juego, se une 4 con 4, 1 con 1, y así sucesivamente. Para el caso de la figura, la suma de los puntos de cada ficha son 4, 5, 6, 7, 8, 9 y están en progresión aritmética, es decir, los números tomados en orden tienen una diferencia común, en este caso particular el 1.

¿De cuántos modos podemos jugar seis fichas de dominó, tomadas de una caja común de veintiocho, para que los números queden en progresión aritmética?

Cuando la edición $N$ de la ONMAS se realiza en un año divisible entre $N$, diremos que es un año superolímpico. Por ejemplo el año 2005 es superolímpico porque se realiza la edición 5 de la ONMAS y 2005 es divisible entre 5. Determina todos los años superolímpicos, sabiendo que la ONMAS se realiza anualmente a partir de 2001 y suponiendo que se seguirá realizando cada año.

Un entero positivo $n$ es aluxe si el producto de los digitos de $n$ es igual al producto de los digitos de $n+1$. ¿Cuántos enteros aluxes hay menores o iguales a 2011 y mayores o iguales a 1?

Se tienen diez monedas indistinguibles en hilera. Se sabe que dos de ellas son falsas y están en posiciones consecutivas en la hilera. Una pregunta consiste en elegir un subconjunto cualquiera de las monedas y preguntar cuántas de ellas son falsas.  Decidir si es posible identificar con certeza las monedas falsas haciendo solamente dos preguntas, sin conocer la respuesta de la primera antes de formular la segunda.