VI ONMAS 2006

Paz hace una lista con todos los números del 1 al 2006. Encierra en un círculo todos los números que son múltiplos de 6. Luego, encierra en un círculo todos los números que son múltiplos de 7. Finalmente, multiplica todos los números que encerró. ¿Cuál es la mayor potencia de 11 que divide exactamente al resultado de esta multiplicación?

Se tiene cierto número de bolsas acomodadas en una fila. En ellas se meten canicas de la siguiente forma: en la primera bolsa se mete una canica, en la segunda bolsa dos, en la tercera tres y así sucesivamente. Luis escoge una bolsa que tiene catorce canicas menos que la última bolsa de la fila y observa que la suma de todas las canicas de las bolsas que están a la derecha de la que escogió es igual a la suma de las que están a la izquierda. ¿Cuántas canicas tiene la bolsa que Luis escogió?

Para cualquier número natural $n$ se dice que su origen se calcula multiplicando sus cifras, después las cifras del resultado, y así sucesivamente hasta llegar a un número de una sola cifra. Por ejemplo, el origen del 149 es el 8, ya que $149\rightarrow36\rightarrow 18\rightarrow 8$; y el origen del 5486 es el 0, ya que $5486\rightarrow 960\rightarrow 0$. Encuentra la suma de todos los números de dos o más cifras distintas, tales que su origen sea un número impar.

Sean $ABC$ un triángulo, y $D$ y $E$ puntos sobre $AC$ y $BC$, respectivamente, tales que $AB$ es paralelo a $DE$. Sea $P$ el pie de la altura trazada desde $A$ al segmento $BC$. Si el ángulo $ACB$ es de 20 grados y $AB = 2DE$, encuentre el valor del ángulo $PDC$.

Encontrar todos los números naturales $n$ tales que sus divisores, distintos de $1$ y $n$, cumplen que el más grande es 7 veces el más pequeño.

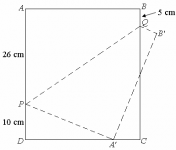
Una hoja de papel en forma rectangular $ABCD$ se dobla a lo largo de la línea $PQ$ de manera que el vértice $A$ quede en el lugar del punto $A’$ y el vértice $B$ en el lugar del punto $B’$. Al medir los segmentos $AP, BQ, DP$, se tiene que miden $26 cm, 5 cm$ y $10 cm$, respectivamente.

¿Cuál es el área del la hoja de papel?