XII ONMAS 2012
Perímetro de hexágono --con dos equiláteros superpuestos
Dos triángulos equiláteros ABC y DEF de perímetros 36 y 27 centímetros, respectivamente, están sobrepuestos, formando un ángulo de 120 grados como se muestra en la figura. Calcula el perímetro del hexágono sombreado.
División sucesiva entre 14 de 2012!
Rosy efectúa la multiplicación 1×2×3×…×2012, luego divide el producto entre 14, y continúa dividiendo --cada uno de los cocientes obtenidos-- entre 14. ¿Cuál es el mínimo número de divisiones que tendrá que hacer Rosy para que el cociente de la división ya no sea un número entero?
Demostrar punto medio --si un ángulo es el triple de otro
Sean W1 y W2 dos circunferencias de centros O1 y O2, respectivamente, que se intersectan en los puntos A y B. El punto C está sobre W1 y es diametralmente opuesto a B. Las rectas CB y CA cortan de nuevo a W2 en los puntos P y Q, respectivamente, donde el punto B está entre C y Q. Las rectas O1A y PQ se intersectan en el punto R. Si la medida del ángulo PBQ es el triple que la del ángulo PCQ, demuestra que AO1=AR
Plantas vs Zombies
En la versión 20.12 del juego Plantas vs Zombies, el campo de batalla es un jardín que se divide en 45 casillas, como se muestra en el dibujo. En esta versión del juego debes colocar en cada casilla una planta o un zombie y ganas si neutralizas el jardín. Para ello debe haber en cualquier cuadro de 2×2 casillas dos plantas y dos zombies. Encuentra el número de acomodos posibles que te permita ganar el juego.
Colocación de fichas en el borde de un tablero
Luis tiene un tablero cudriculado con la misma cantidad de filas que de columnas. Las casillas del contorno del tablero están coloreadas de gris. También tiene suficientes fichas numeradas (1,2,3,...) que coloca en las casillas grises de la siguiente manera:
La ficha 1 la pone en la casilla izquierda y, a partir de ahí, el resto las coloca una en cada casilla, consecutivamente de menor a mayor en sentido de las manecillas del reloj. Una vez que llega a la posición inicial sigue colocando fichas sobre las que ya están puestas. Deja de poner fichas cuando observa que los números que están a la vista en las casillas de las esquinas del tablero suman 2012.
Problemas del segundo dia del nacional 12 ONMAS
Números Paceños
Se dice que un número es Paceño si al escribir sus dígitos en orden inverso se obtiene un número mayor que él. Por ejemplo, el 3426 es Paceño porque 6243 es mayor que 3426, mientras que el 774 no es Paceño porque 477 no es mayor que 774. ¿Cuántos números de cinco dígitos son Paceños?
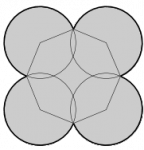
Diferencia de áreas de flores en octágono
A partir de un octágono regular de lado 10 cm, Anita dibuja dos flores como se muestran a continuación:
¿Cuál es la diferencia entre las áreas de las flores?
Juego de números en un tablero romboidal
En cada rombo de la figura se coloca un número diferente del 1 al 9. Enseguida, dentro de los círculos se escribe la suma de los dos números que comparten ese lado. Finalmente, se suman los números escritos en los círculos.
De todas las sumas posibles ¿cuál es la diferencia entre la mayor y la menor?

Tesoro de Hernán Cortés --en 2012 cofres
En la Bahía de la Paz, Hernán Cortés guardó su tesoro en 2012 cofres con sus respectivos candados. Cada candado y su cofre están numerados del 1 al 2012. Cortés metió al azar una llave en cada cofre y cerró los candados para que nadie tomara el tesoro. Mucho tiempo después, se halló el tesoro de Cortés. Los arqueólogos van a forzar los candados marcados con los números 1 y 2 para obtener así dos de las llaves con la esperanza de que con ellas sea posible abrir sucesivamente todos los demás cofres. ¿De cuántas maneras pudieron quedar distribuidas inicialmente las llaves dentro de los cofres de manera que la estrategia de los arqueólogos sea exitosa?
