Álgebra

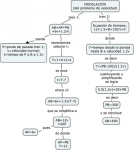
En este post comento dos problemas de velocidad ya en la sección de problemas de MaTeTaM. Le dedico más tiempo al más difícil, tratando de destacar la lógica de su solución. Al final presento un mapa conceptual del razonamiento y la simbolización del difícil, el cual parecería le da más estructura al proceso de resolución.

La computadora, se ha dicho, es una solución en busca de problemas. Y en la enseñanza de las matemáticas se postuló, desde la aparición de esa herramienta maravillosa, que la PC (y, antes de ella, las calculadoras) podría ser la solución a las dificultades que los estudiantes enfrentan al aprender esa "ciencia incomprensible" (la etiqueta es espuria, pero de aceptación universal) denominada álgebra .

En el paper Developing Katy's Algebraic Structure Sense, Hoch y Dreyfus, los autores de este reporte de investigación, someten a prueba empírica un método de enseñanza individualizada de las matemáticas que podríamos llamar "entrevistas didácticas" (teaching interviews).

Los autores usan las entrevistas didácticas para mejorar el desempeño en matemáticas de adolescentes que, si bien son buenos en la manipulación algebraica, no han adquirido el  "sentido de la estructura". Eligieron para ilustrar los resultados a Katy, una adolescente de 16 años.

Es bien conocido dentro de la educación matemática que, en sus orígenes, el álgebra no usaba símbolos sino que el problem solving se describía totalmente utilizando el lenguaje natural. A esta etapa del álgebra se le llama fase retórica (antes de Diofanto). Después vendría la fase sincopada o lacónica, la cual se habría dado entre Diofanto y Vieta  y,  finalmente, llegaría la fase simbólica que inicia con Vieta. (Se dice que fue un alemán del siglo XIX quien primero identificó y nombró las tres fases del desarrollo del álgebra.)

Ahora que está de moda hablar (en educación matemática) de matematizar, situaciones reales o formales, como una vía para enseñar matemáticas en la escuela, puede ser de alguna utilidad tematizar este verbo en un post de MaTeTaM. Ver mi post sobre Letracidad Matemática

Dos preguntas tipo del examen ENLACE

En estos días de septiembre, en que aparecieron ya los resultados del examen ENLACE 2009, me puse a buscar en la Web el tipo de preguntas de matemáticas que se le hicieron al adolescente en abril --para ponderar su grado de dificultad y poder generar así una opinión informada sobre su pésimo desempeño en ese examen. Encontré solamente dos preguntas tipo, las cuales reproduzco y comento a continuación (el título de las preguntas es mío). Se pueden consultar en http://www.sepdf.gob.mx/principal1/archivos/ENLACE%202009.pdf