Solución diagramática
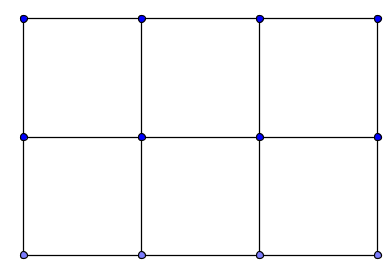
Los datos sugieren tomar como unidad de trabajo media cuadrilla en media jornada. Porque toda la cuadrilla son dos medias cuadrillas. Así que dos medias cuadrillas en la mañana y media cuadrilla en la tarde acabaron el prado grande. Esto sugiere dividir el prado grande en tercios: media cuadrilla en media jornada termina 1/3 del prado grande. Pero el prado chico es la mitad del prado grande, y conviene dividir el prado grande en sextos. Esto significa que media cuadrilla en la tarde cortó 2/3 del prado chico (igual a 2/6=1/3 del grande. Ver figura.) Y quedó 1/3 del prado chico sin cortar. Esta tarea la ejecutó un solo jardinero en dos medias jornadas, lo cual equivale a decir: dos jardineros en media jornada. Pero toda la cuadrilla termina 4 de estos cuadros en media jornada (porque toda la cuadrilla corta 2/3 del prado grande en media jornada). Es decir, la cuadrilla era de 8 jardineros (se necesitan cuatro veces dos jardineros para terminarlo).
Solución algebraica
Si uno no desea pensar, se pone en automático y deja que el algebra haga el trabajo. Porque si la cuadrilla se compone de 2n jardineros, entonces (2n+n)E=2A y (n+2)E=A --donde E es la eficiencia de cada jardinero en media jornada (i.e, la fracción de A que corta en media jornada), y A es el área del prado chico. Y se ve que n=4 (después de resolver el sistema --donde, por cierto, se elimina E) . Es decir, la cuadrilla era de 8 jardineros. (El álgebra es maravillosa ¿no es cierto? Pero uno se puede poner en automático gracias a haber adquirido antes la habilidad de modelación y la de resolución de ecuaciones --unas habilidades cuya adquisición no sucede de manera espontánea...)
Solución con razonamiento de sentido común
Prado grande:
Mañana: 2n (todos) en 4 horas hacen una fracción de 2A.
Tarde: n (la mitad) en 4 horas hacen la fracción de 2A que faltaba.
Por tanto, 3n harían 2A (el prado grande) en 4 horas. (Principio utilizado: 2n en la mañana y n en la tarde es lo mismo que 3n en la mañana.)
Prado chico:
Tarde: n (la mitad) en 4 horas hacen una fracción de A (prado chico).
Al otro día: 2 (uno en 8 horas) hacen la fracción restante de A.
Por tanto, n+2 harían A en 4 horas. (Principio utilizado: n en la tarde y 1 todo el día es lo mismo que n+2 en la tarde.)
En consecuencia, 2n+4 harían 2A en 4 horas. (Principio utilizado: el doble hacen el doble.)
Conclusión: Pero entonces 2n+4=3n. Es decir, n=4. La respuesta es entonces que la cuadrilla (2n) es de 8 jardineros.
Nota: una de las razones de que el problema sea clásico es que requiere un mínimo de matemáticas.

La solución diagramática está
La solución diagramática está inspirada por la solución de uno de los concursantes. El problema se cataloga como intermedio, debido al hecho de que la proporcionalidad inversa siempre ha sido difícil para todos los niveles. Lo que trataba de medir en el estatal es la capacidad de razonamiento del aspirante a preseleccionado. No es en sí problema de concurso típico. Pero si un adolescente es capaz de traducir a un modelo algebraico el enunciado, o razonar el problema como en la solución diagramática, por ese solo hecho merece estar en la preselección. Por otro lado, el problema es clásico --es decir, se puede encontrar en los libros de texto actuales. En otras palabras, ha sobrevivido al tiempo a pesar de ser muy viejo; éste es el significado de clásico.
Los saluda
(En la foto yo soy el de
(En la foto yo soy el de arriba)
Yo deduzco que la cuadrilla completa hizo 4/3x2 y media cuadrilla 2/3x2, por lo que sobro 1/3x2 el cual lo hizo un jardinero solo en 8 horas por lo que lo multiplico por 1/8 para obtener cuanto hace por hora y obtengo 1/24x2, los 4/3x2 los multiplico por 1/4 para obtener cuanto hace la cuadrilla completa en una hora y obtengo 4/12x2.
Divido 4/12x2 entre 1/24x2 para obtener el total de la cuadrilla y obtengo 8 jardineros que la integran.
Tu solución es muy buena.
Tu solución es muy buena. Sólo tienes que explicar cómo llegas a ver sextos. (Creo que el método que usas se llama "del elemento unitario" y se usa en problemas de proporcionalidad --y se enseña en secundaria. Vaya una felicitación para tí por aprenderlo correctamente y a tus maestros de matemáticas por enseñártelo también correctamente --bueno, en esta época uno tiene que felicitar a las personas por hacer lo que se supone que deberían hacer, dado que en el noventaynueve punto coma porciento no se cumple con las obligaciones y el hecho de que alguien las cumpla ya es un hecho extraordinario...)
Te saluda
PD: tu razonamiento es muy claro y directo y eso es también un hecho extraordinario...
Muchas gracias, pero creo que
Muchas gracias, pero creo que el merito se debe mas a la asesoria que nos dio el Ing. Alcocer, y creo que debe estar muy contento , porque la mayoria de los que el maestro asesoro (LA ZONA SUR) quedaron en el concurso, a si que muchas felicitaciones.
SALUDOS A TODOS.....
Att. Luis german diaz zuñiga.
Esc. sec. gral. 1 Lic. Benito Juarez Garcia, Altamira, Tamps.
OK Germán, pero ¿cómo llegas
OK Germán, pero ¿cómo llegas a los sextos en tu solución? (Así como la pusiste no creo que te hubieran dado los 7 puntos.)
NO UTILICE SEXTOS, UTILICE
NO UTILICE SEXTOS, UTILICE TERCIOS, PUES NOMBRE AL PRADO CHICO CON EQUIS CUADRADA Y AL PRADO GRANDE CON DOS EQUIS CUADRADA(EL PRADO GRANDE TIENE EL DOBLE DE AREA QUE EL CHICO).
EN EL PRADO GRANDE ESTUVIERON LAS PRIMERAS CUATRO HORAS TODA LA CUADRILLA COMPLETA Y LAS SIGUIENTES CUATRO HORAS LA MEDIA CUADRILLA POR LO QUE ENTONCES TOMANDO EN CUENTA QUE LA EFICIENCIA ES CONSTANTE E IGUAL PARA TODOS LOS JARDINEROS ENTONCES LA CUADRILLA COMPLETA HIZO DOS TERCIOS DE DOS EQUIS CUADRADA, LOS CUALES AL MULTUPLICARLOS, OBTENEMOS CUATRO TERCIOS DE EQUIS CUADRADA, Y LA MEDIA CUADRILLA HIZO UN TERCIO DE DOS EQUIS CUADRADA QUE ES IGUAL A DOS TERCIOS DE EQUIS CUADRADA, LOS 4 TERCIOS DE EQUIS CUADRADA LOS MULTIPLICO POR UN CUARTO PARA OBTENER CUANTO HACE LA CUADRILLA POR HORA, Y OBTENGO 4/12 DE EQUIS CUADRADA...
TOMANDO QUE LA OTRA MEDIA CUADRILLA ESTUVO EN EL PRADO CHICO, Y QUE ESTA HACE DOS TERCIOS DE EQUIS CUADRADA, AL RESTARLE EL AREA DEL PRADO CHICO, OBTENGO COMO RESIDUO UN TERCIO DE EQUIS CUADRADA, QUE FUE LA QUE HIZO UN JARDINERO EN 8 HORAS, POR LO QUE UN TERCIO DE EQUIS CUADRADA LO MULTIPLICO POR UN OCTAVO PARA OBTENER CUANTO HACE UN JARDINERO POR HORA Y OBTENGO 1/24 DE EQUIS CUADRADA.
AHORA LO QUE HAGO ES DIVIDIR 4/12 DE EQUIS CUADRADA QUE ES LO QUE HACE LA CUADRILLA COMPLETA EN UNA HORA ENTRE 1/24 DE EQUIS CUADRADA QUE ES LO QUE HACE UN JARDINERO EN UNA HORA Y OBTENGO 96/12 QUE ES IGUAL A 8. POR LO CUAL LA CUADRILLA COMPLETA ESTABA COMPUESTA POR 8 JARDINEROS.
SALUDOS Y MUCHAS GRACIAS POR SUS OBSERVACIONES...
ATT. LUIS GERMAN DIAZ ZUÑIGA.
Esc. Sec. Gral. N 1 Lic. Benito Juarez Garcia, Altamira, Tamps.
OK. Ya entendí: cuando tú
OK. Ya entendí: cuando tú escribes 4/3x2 quieres decir (4/3)x^2. Yo supuse que habías querido escribir 4/(3x2) o sea 4/6. De cualquier manera tu escritura matemática estaba incorrecta pero en otro sentido.
Recomendación: los exponentes como el 2 de x2 ponlos con el símbolo ^ (no creo que se te dificulte encontrarlo en tu teclado) y después la expresión x^2 la encierras entre signos de pesos (abres y cierras) y ya te aparece la expresión correcta x2. Inténtalo por favor.
Te saluda