Denotemos con (ABC) el área del triángulo ABC. Los triángulos CDA y DBA tienen la misma altura de A, y los CDP y DBP tienen la misma altura de P. De aquí que CD/DB=(CDA)/(DBA)=(CDP)/(DBP). Entonces, por un lado, CD/DB=(s+t+2)/(m+1) y, por el otro, CD/DB=s. Es decir, s=(s+t+2)/(m+1). De manera similar, t/2=(s+t+1)/(m+2).
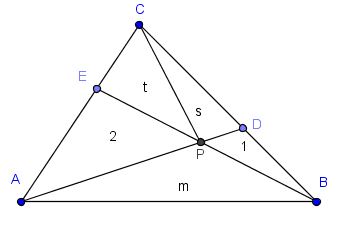
Ahora bien, del enunciado se concluye que s+t es entero (dado que m es entero y el área de ABC también). De aquí que n=s+t=(s+t+2)/(m+1)+2(s+t+1)/(m+2)
=(n+2)/(m+1)+2(n+1)/(m+2)
=[(m+2)(n+2)+2(m+1)(n+1)]/[(m+1)(m+2)].
Despejando n se obtiene la ecuación n=2(2m+3)/(m2−2). Puesto que n es entero positivo, se concluye que m2−2 es menor o igual que 4m+6. De aquí se logra, completando el trinomio cuadrado perfecto, (m−2)2 menor o igual que 12 y, entonces, m sólo puede tomar los valores 1,2,3,4,5.
Ahora damos valores a m y calculamos n. El único valor de m que da n entero es m=2, lo cual resulta en n=7. Así que, en resumen, (ABC)=1+2+2+7=12.

El problema es difícil.
El problema es difícil. Primero porque hay que modelarlo algebraicamente. Pero antes de llegar a ello hay que saber el hecho de que la razón de las bases es igual al de las áreas cuando los triángulos comparten un vértice. Un hecho básico, pero no lo es tanto si no se ha practicado en la resolución de problemas. Ahora bien, suponiendo que ya se modeló algebraicamente, lo que sigue es la solución del modelo lo cual requiere saber álgebra en el sentido procedimental.
Pero también requiere acotar y hacer inferencias sobre la integridad de algunos números. Una dificultad adicional es que, en la manipulación algebraica, es muy fácil cometer errores al pasar de una ecuación a la siguiente. Esto evaluaría también la destreza algebraica del adolescente.
Desglose y criterios de evaluación sugeridos
a) Plantear las proporciones lados-áreas (1 punto)
b) Usarlas para planear dos ecuaciones con las áreas como variables (1 punto)
c) Plantear la ecuación de las áreas y ahí abandonar (1 punto)
d) Acotar (2 puntos) pero ya no saber qué hacer e) Obtener la solución (2 puntos) f) Obtener la solución por algún otro método pero bien justificada (7 puntos).
Los saluda
jmd
PD: después del examen se reveló que es un problema muy difícil pues nadie lo resolvió; posiblemente porque parece de geometría pero es también algebraico y tiene algo de números.