Sea dada una circunferencia c de centro O y radio r, y un punto P fuera del círculo. Demostrar que el siguiente procedimiento produce el inverso P' de P con respecto a la circunferencia c.
1) Trazar la recta OP.
2) Trazar una de las tangentes desde P a c, y llamar T al punto de tangencia.
3) Bajar desde T una perpendicular a OP y llamar P' al pie de esa perpendicular.
4) P' es el inverso de P respecto a c.
Ver también:
Inversión (en geometría)
Ver también:
Altura de un triángulo rectángulo 
Para que se cumpla que es P'
Para que se cumpla que es P' es inverso de P debemos demostrar que r^2=(OP)(OP'), lo cual es sencillo Veamos la figura: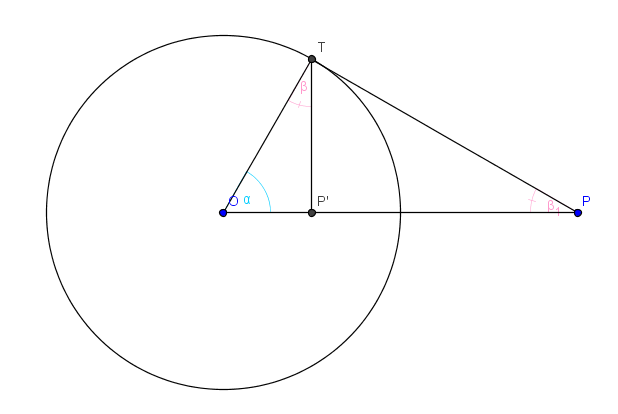
Tenemos que los triangulos OP'T~OTP; notemos que ambos tienen un angulo α y un angulo recto; y por tanto tambien tienen un angulo β entonces podemos afirmar que exsisten las razones: OP'/OT=P'T/TP=OT/OP; donde OT=r entonces tenemos que OP'/r=r/OP entonces: OP'(OP)=r^2, por lo tanto P'es el inverso de P respecto a c
PD;el problema tiene un error de dedo; dice "Trazar una de las tangentes desde A a c y llamar T al punto de tangencia" pero deberia decir desde P; hah en fin; cmo qiera se entiende; mm.. nunca me habia puesto a leer sobre inversion; parece interesante; Otra cosa; tengo una duda; nada que ver con el problema; sino respeccta a la pagina; porque se ve asi? Acaso es el nuevo diseño? Yo llegue a pensar que era mi compu; pero no; en fin; Saludos:D
Gracias por la corrección y
Gracias por la corrección y por la solución. Ponla por favor como solución. Creo que tienes los permisos de colaborador...
Te saluda
Creo que no... quizaas me
Creo que no... quizaas me equivoco; y no se como hacerle; haaha'
Saludos;
Sadhi(: