Publicaciones Recientes
El diagrama: ¿facilita realmente el razonamiento?
La respuesta a la pregunta del título es: depende del razonador. Esta respuesta la derivé de una experiencia de enseñanza que a continuación narro y comento.
En estos días, dentro del tema de geometría, traté de enseñarles a dos jóvenes universitarios el teorema de Pitágoras. Es decir, la demostración de ese famoso teorema. Fue de hecho un experimento didáctico, solamente para comprobar que a un estudiante profesional (es decir, que el ser estudiante ha sido su modus vivendi por al menos 13 años) le resulta casi imposible concentrarse en una tarea de este tipo.

Cuerdas y concurrencia
Sean PQ, RS y TU cuerdas de una circunferencia tales que PQ=RS=TU, y éstas no se intersectan dentro de la circunferencia. UP corta a QR en A, QR corta a ST en B y ST corta a UP en C. Sean L, M y N los puntos medios de PQ, RS y TU respectivamente. Demostrar que AL, BM y CN son concurrentes.
Competencias comunicativas y cognitivas en la RIEMS
Como se sabe (o se debería saber) el razonamiento está ligado al lenguaje, en particular a la competencia lingüística del hablante. La hipótesis dominante en esta área de la investigación científica es la de Vygotsky: lenguaje y pensamiento son interdependientes (es decir, se determinan mutuamente). (Esta hipótesis ha dado origen a la psicolingüística.) Otras posiciones (hipótesis) son posibles y todas han sido posiblemente defendidas por los estudiosos de la filosofía y la lingüística.
Acertijo lógico con tres variables dicotómicas
El exitoso empresario X, rico de nacimiento, quiere contratar los servicios de un guardaespaldas para proteger su persona de la delincuencia organizada. Para ello habla con el director de la agencia Z, especializada en ese tipo de contrataciones.
Pensar matemáticamente
Ahora que está de moda hablar (en educación matemática) de matematizar, situaciones reales o formales, como una vía para enseñar matemáticas en la escuela, puede ser de alguna utilidad tematizar este verbo en un post de MaTeTaM. Ver mi post sobre Letracidad Matemática
Malas noticias: no le llegamos al oro (Brandon 26, corte en 34)
Ahora que la selección Tamaulipas llevaba el mejor (como nunca), y en el cual habíamos puesto todas nuestras esperanzas, el oro se mostró negado para Tamaulipas (como siempre). Y veo difícil que se vuelva a formar otro Brandon en el corto plazo --a menos que... bueno Ramón sabrá cómo hacerle...
Otra forma de ver Cauchy
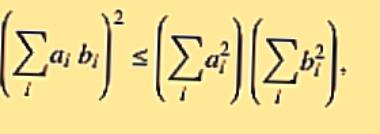
Resultados parciales de la selección Tamaulipas
Problema 1 Problema 2 Problema 3 Problema 4 Problema 5 Proble
Noticias de Campeche
Como ya se dieron cuenta ya están en MaTeTaM los problemas del concurso nacional de la Olimpiada Mexicana de Matemáticas en su versión 2009. Según comunicado de Ramón el examen estuvo muy difícil (en opinión generalizada) y tenemos los siguientes pronósticos:
--Casanova, mención :(
XXIIIOMM Problema 6
En una fiesta con n personas se sabe que de entre cualesquiera 4 personas, hay 3 de las 4 que se conocen entre sí o hay 3 que no se conocen entre sí. Muestra que las n personas se pueden separar en 2 salones de manera que en un salón todos se conocen entre sí y en el otro salón no hay dos personas que se conozcan entre sí.
