Publicaciones Recientes
XIV ONMAPS (primer día)
Esta semana se realizó en Mazatlán la XIV Olimpiada de Matemáticas para Alumnos de Primaria y Secundaria (ONMAPS). El lunes 19 los concursantes resolvieron la primera parte, y el martes la segunda. En cada una, el examen consistió de 6 problemas y los concursantes debían resolver 3 según su nivel o categoría:
Primaria resolvió los problemas 1,2,3.
Primer grado los problemas 2,3,4.
Segundo grado los problemas 3,4,5.
Tercer grado los problemas 4,5,6.
Los problemas del primer día son los siguientes:
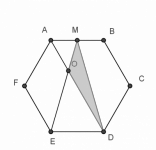
cuadrado ABCD
En un cuadrado ABCD, se coloca un punto intermedio en cada uno de sus lados y llamarlos EFGH, unir FG,FE,EH Y Hg, luego unir AF y DB y en la intersecion colocar x, demostrar que al unir x con H y con G los segmentos son iguales
Ejercicio en matemáticas del reloj
Ejercicio en diferencia de cuadrados
La diferencia de dos números es 2 y la diferencia de sus cuadrados es 8. ¿Cuánto vale su suma?
Recuerdos de Querétaro 1998
Encontrar los enteros positivos mínimo (m) y máximo (M) que se pueden expresar en la forma $1/a_1+2/a_2+3/a_3+...+9/a_9$ (Donde $a_1,...,a_9$ son dígitos, no necesariamente distintos.)
Suertudos
Un número se dice que es suertudo si al sumar los cuadrados de sus cifras y repetir esta operación suficientes veces se obtiene el número 1. Por ejemplo el número 1900 es suertudo, pues en la primera operación se obtiene 82, en la segunda 64+4=68, en la tercera se obtiene 100 y en la cuarta se obtiene el 1. Encontrar dos números consecutivos que sean suertudos.
3m+2 nunca es cuadrado perfecto
Sea m un entero. ¿Puede ser cuadrado perfecto un número de la forma 3m+2?
Ejercicio de asociación de ideas
Calcular el valor de $x^3+1/x^3$ si se sabe que $x+1/x=9$.
Ejercicio de reconocimiento de un producto notable
Calcular el valor de
$$\frac{2x+8}{\sqrt{2x+1}+\sqrt{x-3}}$$
si se sabe que $\sqrt{2x+1}-\sqrt{x-3}=2$.
Ejercicio con rectángulo y punto medio
En un rectángulo ABCD, M es el punto medio de BC. Si T es el pie de la perpendicular a AM bajada desde D demostrar que CT=CD.
